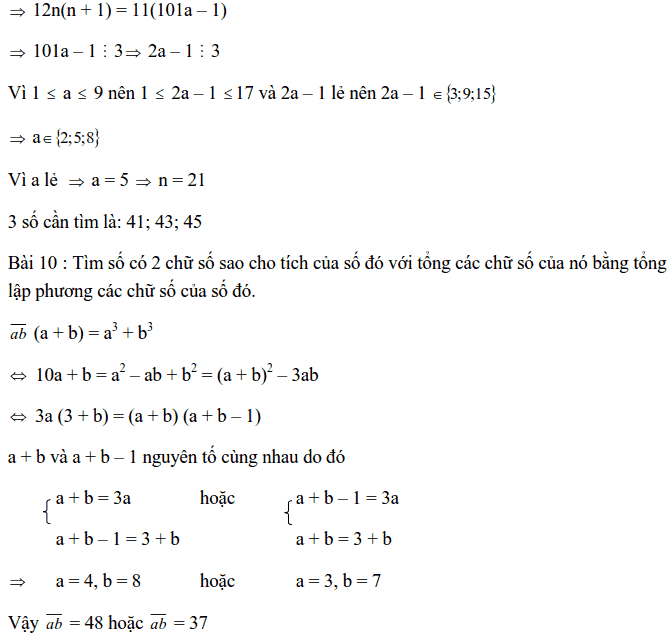I- ĐỊNH NGHĨA
Số chính phương là số bằng bình phương đúng của một số nguyên.
II- TÍNH CHẤT
1- Số chính phương chỉ có thể có chữ số tận cùng bằng 0, 1, 4, 5, 6, 9; không thể có chữ tận cùng bằng 2, 3, 7, 8.
2- Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.
3- Số chính phương chỉ có thể có một trong hai dạng 4n hoặc 4n+1. Không có số chính phương nào có dạng 4n + 2 hoặc 4n + 3 (n ∈ N).
4- Số chính phương chỉ có thể có một trong hai dạng 3n hoặc 3n +1. Không có số chính phương nào có dạng 3n + 2 (n ∈ N).
5- Số chính phương tận cùng bằng 1, 4 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2.
Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
6- Số chính phương chia hết cho 2 thì chia hết cho 4.
Số chính phương chia hết cho 3 thì chia hết cho 9
Số chính phương chia hết cho 5 thì chia hết cho 25
Số chính phương chia hết cho 8 thì chia hết cho 16.
III- MỘT SỐ DẠNG BÀI TẬP VỀ SỐ CHÍNH PHƯƠNG
Mục lục
Dạng 1: CHỨNG MINH MỘT SỐ LÀ SỐ CHÍNH PHƯƠNG


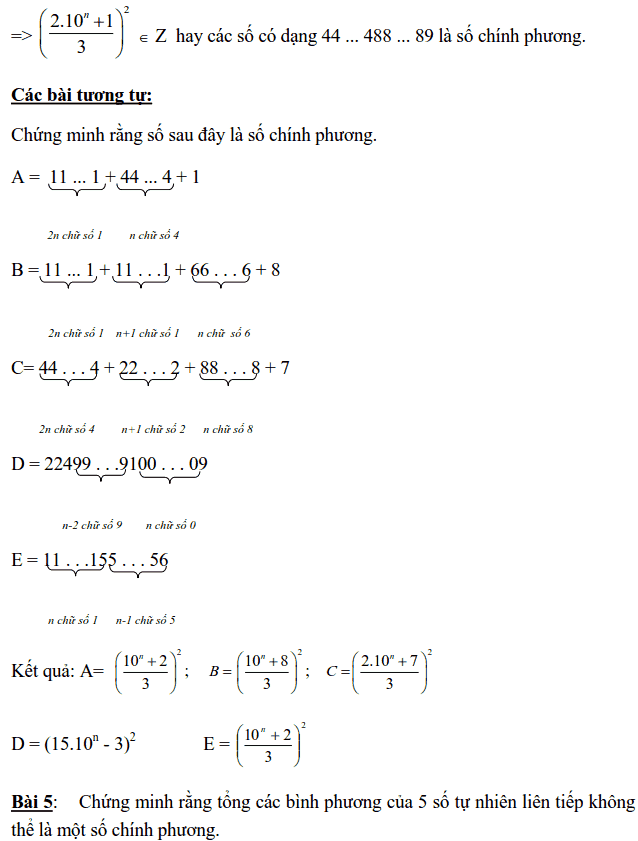
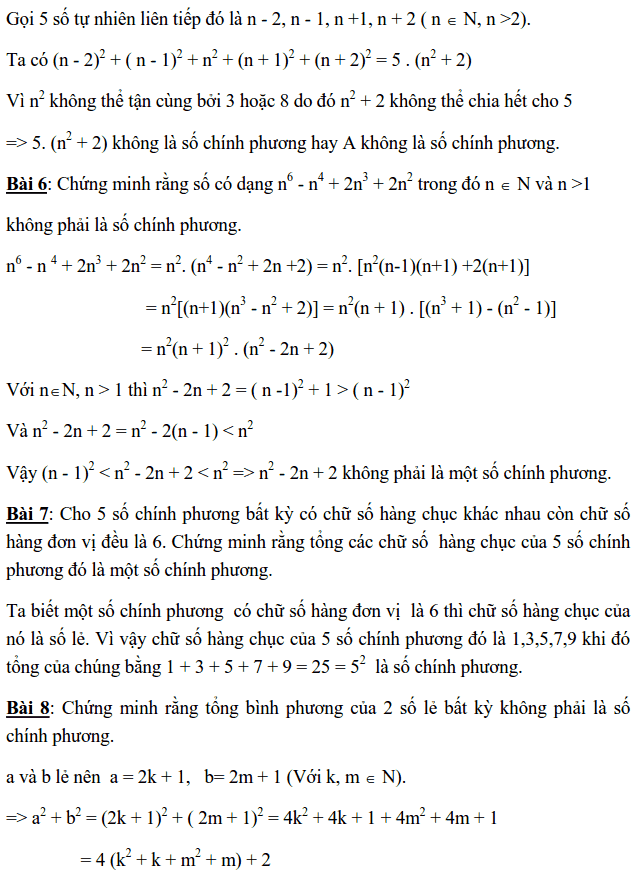


Dạng 2: TÌM GIÁ TRỊ CỦA BIẾN ĐỂ BIỂU THỨC LÀ SỐ CHÍNH PHƯƠNG




Dạng 3 : TÌM SỐ CHÍNH PHƯƠNG