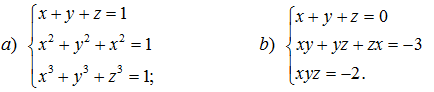Phương trình quy về phương trình bậc hai Toán 9
Kiến thức cần nhớ:
Nhiều phương trình có thể giải bằng cách quy về phương trình bậc hai như phương trình bậc cao hơn bậc hai, phương trình chứa ẩn ở mẫu thức, phương trình vô tỉ,…
Phương pháp đưa về phương trình tích và phương pháp đặt ẩn phụ thường được dùng để giải các phương trình loại này.
Mục lục
I. PHƯƠNG TRÌNH CHỨA ẨN TRONG DẤU GIÁ TRỊ TUYỆT ĐỐI
Ví dụ 27. Giải phương trình:

Ví dụ 28.
Giải phương trình:
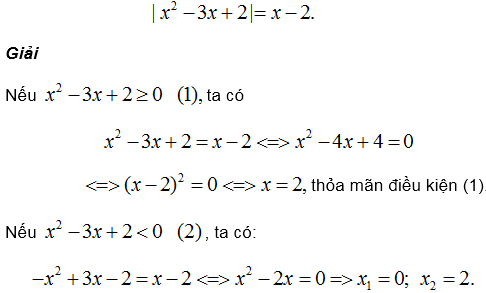
Cả hai giá tị này đều không thỏa mãn điều kiện (2).
Vậy phương trình có nghiệm duy nhất x = 2.
II. PHƯƠNG TRÌNH BẬC CAO
Phương trình bậc cao thường được giải bằng cách đưa về phương trình tích hoặc dùng ẩn phụ. Cần chú ý đến các dạng sau:

Ví dụ 29. Giải phương trình:
$3 x^{4}+2 x^{3}-34 x^{2}+2 x+3=0$ (1)
Giải
Phương trình trên là phương trình đối xứng (các hệ số có tính đối xứng).
Hiển nhiên = 0 không là nghiệm của phương trình (1). Chia hai vế của phương trình 91) cho ta được
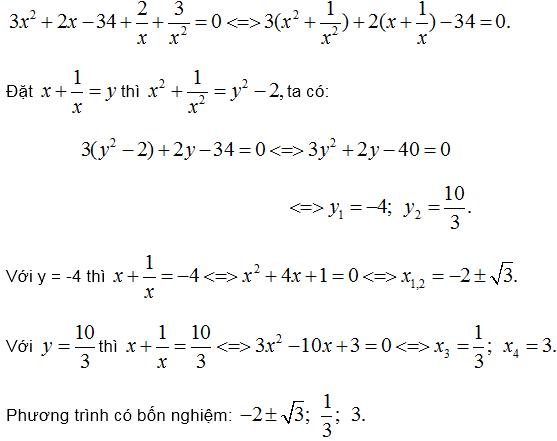
Chú ý:
a) Trong phương trình đối xứng, nếu a là nghiệm thì cũng là nghiệm.
b) Phương trình đối xứng bậc lẻ bao giờ cũng có một trong các nghiệm là x = -1.
c) Phương trình đối xứng bậc chẵn 2n được đưa về phương trình bậc n bằng cách đặt ẩn phụ y = x .
Ví dụ 30. Giải phương trình
(12x – 1)(6x – 1)(4x – 1)(3x – 1) = 330.
Giải
Trước hết ta biến đổỉ phương trình để hệ số của x trong các dấu ngoặc đều bằng nhau :
Nhân các thừa số ở vế trái theo thứ tự với 2, 3, 4.
(12x – 1)(12x – 2)(12x – 3) (12x – 4) – 330.2.3.4.
Đặt 12x – 3 = y, ta có:
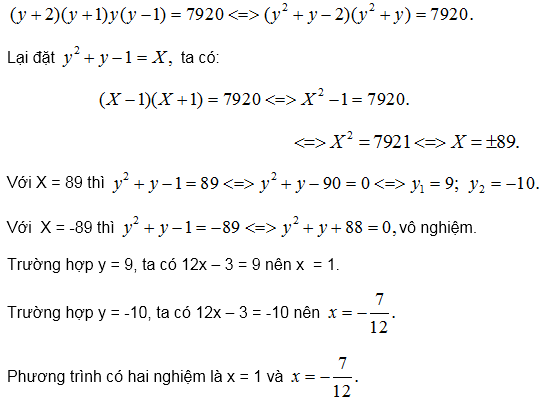
IV. PHƯƠNG TRÌNH VÔ TỈ
Ta gọi các phương trình chứa ẩn trong dấu căn là phương trình vô tỉ. Để giải phương trình vô tỉ chửa căn bậc hai, ta thường khử dấu căn bậc hai bằng cách bình phương hai vế hoặc đặt ẩn phụ.
Ví dụ 32. Cho phương trình
= x – 7 (1)
Một học sinh giải phương trình trên như sau :
Điều kiện để căn thức có nghĩa
x ≥ 5 (2)
Bình phương hai vế của phương trình :
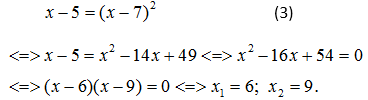
Các giá trị trên thoả mãn điều kiện (2). Vậy phương trình có hai nghiêm là x = 6, x = 9.
Cách giải trên có đúng không ?
Giải
Cách giải trên không đúng vì x = 6 không phải là nghiệm của phương trình (1). Thật vậy, với x = 6, vế trái của phương trình (1) bằng 1, vế phải bằng -1.
Có sai lầm trên là do các phương trình (1) và (3) không tương đương. Khi giải bình phương hai vế của phương trình (1), ta được phương trình (3) là phương trình hệ quả của phương trình (1). Nghiệm của phương trình (1) là nghiệm của phương trình (3) nhưng không đảm bảo điều ngược lại.
Muốn tránh sai lầm trên, ta phải thử các nghiệm của phương trình (3) vào phương trình (1), chỉ có giá trị x = 9 nghiệm đúng phương trình (1).
Việc thử giá trị của ẩn vào phương trình ban đầu nhiều khi không đơn giản. Ta thường thay công việc này bằng cách đặt thêm điều kiện
x – 7 ≥ 0 (2′)
Với điều kiện này, hai vế của phương trình (1) không âm, do đó khi binh phương hai vế, các phương trình (1) và (3) tương đương với nhau.
Lời giải đúng như sau :
Cách 1.
= x – 7 (1)
Điều kiện để căn thức có nghĩá :
x ≥ 5 (2)
Với điều kiện x ≥ 7 (2′), phương trình (1) tương đương với :
x – 5 = (3)
Giải phương trình (3), ta được :
= 6, không thoả mãn điều kiện (2′) ;
= 9, thoả mãn các điều kiện (2) và (2′).
Nghiệm duy nhất của phương trình (1) là x = 9.
Chú ý : Trong cách giải trên ta đặt điều kiện (2) vì “lí do sư phạm”. Thực ra không cần điều kiện này. Thật vậy, khi bình phương hai vế của (1), biểu thức x – 5 bằng một bình phương, đương nhiên không âm, do đó các giá trị của x thoả mãn phương trình (3) cũng sẽ thỏa mãn điều kiện (2).
Cách 2. (đặt ẩn phụ)
Biến đổi phương trình (1) về dạng
= x – 5 – 2.
Đặt y = ≥ 0, ta có y =
– 2.
Giải phương trình – y – 2 = 0, ta được :
= -1 (loại),
= 2.
Với y = 2 ta có
= 2 <=> x – 5 = 4 <=> x = 9.
Phương trình (1) có nghiệm duy nhất x = 9.
Ví dụ 33. Giải phương trình
Giải
Điều kiện để các căn thức có nghĩa :
3x 7 ≥ 0, x 1 ≥ 0 <=> x ≥ -1 (1)
Chuyển vế =
2.
Hai vế của phương trình không âm, ta bình phương hai vế :
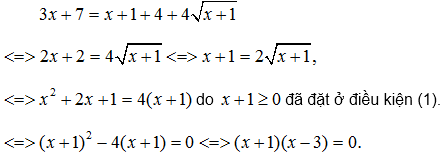
= -1;
= 3. Cả hai giá trị này đều thoả mãn điều kiện (1) và là nghiệm của phương trình.
Chú ý. Trong cách giải trên, ta đã chuyển vế để mỗi căn thức ở một vế.
Cách giải này đơn giản hơn nhiều so với cách bình phương hai vế của phương trình đã cho (bạn đọc tự kiểm nghiệm).
Ví dụ 34. Giải phương trình
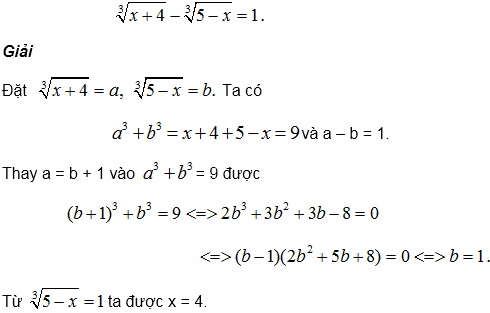
BÀI TẬP
174. Giải các phương trình:
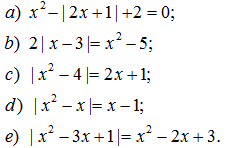
175. Giải các phương trình:
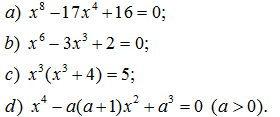
167. Giải các phương trình:
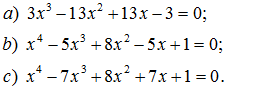
177. Cho biểu thức:
$A = x(x+1)(x+2)(x+3)$.
a) Tìm x để A = 3.
b) Tìm x để A có giá trị nhỏ nhất.
178. Giải các phương trình:
a) $(x+3)^{4}+(x+5)^{4}=16$ b) $x(x+1)(x+2)(x+3)=8$
179. Giải các phương trình:
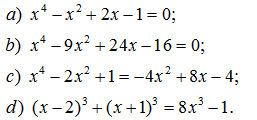
180. Giải các phương trình:
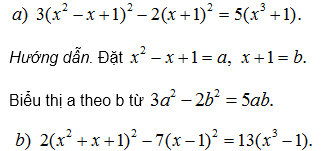
181. Giải các phương trình:
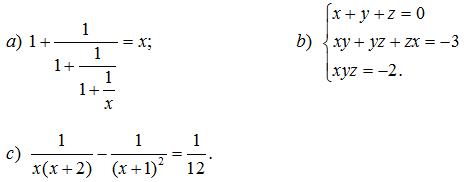
182. Giải các phương trình:
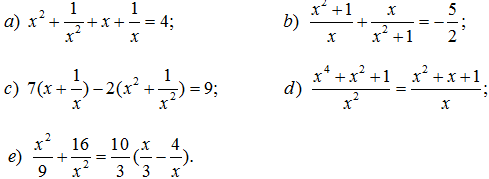
183. Giải các phương trình:
a) $\sqrt{x+2}=4-x$ b) $\sqrt{x^{2}+1}=5-x^{2}$
184. Giải các phương trình:
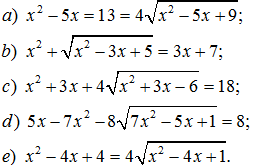
185. Giải các phương trình:
a) $\sqrt{15-x}+\sqrt{3-x}=6$ b) $\sqrt{x+2}-\sqrt{x-6}=2$
186. Giải các phương trình:
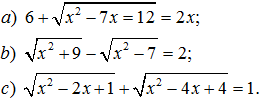
187. Giải các phương trình:
a) $\sqrt{x-2-2 \sqrt{x-3}}$ $\left.b^{*}\right) \sqrt{x+\sqrt{x+11}}+\sqrt{x-\sqrt{x+11}}=4$
188. Giải các phương trình:
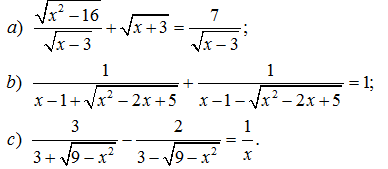
189*. Giải các phương trình:
a) $\sqrt[3]{27+x}+\sqrt[3]{1-x}=4$ b) $\sqrt[3]{10+x}+\sqrt{26-x}=6$
190. Giải các hệ phương trình:
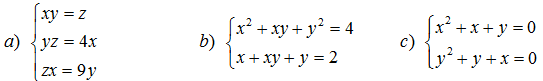
191. Giải các hệ phương trình:

192*. Giải các hệ phương trình: