Các bài toán hình ôn thi vào lớp 10 không chuyên có lời giải

Tài liệu này gồm các bài toán hình ôn thi vào lớp 10 dành tặng cho các em học sinh lớp 9 đang chuẩn bị ôn thi vào lớp 10 không chuyên.

Với mỗi bài toán Hình học sẽ có lời giải chi tiết kèm theo lời bàn (hướng dẫn cách suy nghĩ giải Toán hình). Mỗi trang Toán cấp 2 trình bày 1 bài tập để các em tiện theo dõi.

(Nguồn tài liệu: sưu tầm)

Bài 1:

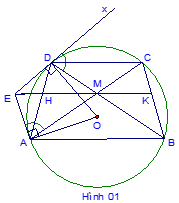
Cho hình thang cân ABCD (AB > CD, AB // CD) nội tiếp trong đường tròn (O). Kẻ các tiếp tuyến với đường tròn (O) tại A và D chúng cắt nhau ở E. Gọi M là giao điểm của hai đường chéo AC và BD.
1. Chứng minh tứ giác AEDM nội tiếp được trong một đường tròn.
2. Chứng minh AB // EM.
3. Đường thẳng EM cắt cạnh bên AD và BC của hình thang lần lượt ở H và K.
Chứng minh M là trung điểm HK.
4. Chứng minh $\frac{2}{HK}=\frac{1}{AB}+\frac{1}{CD}$

BÀI GIẢI CHI TIẾT (hình 01)

1. Chứng minh tứ giác AEDM nội tiếp

Ta có: $\widehat{EAC}=\frac{1}{2}$sđ$\stackrel{⌢}{AC}$  (góc tạo bởi tia tiếp tuyến AE và dây AC của đường tròn (O))

Tương tự: $\widehat{xDB}=\frac{1}{2}$sđ$\stackrel{⌢}{DB}$  (Dx là tia đối của tia tiếp tuyến DE)

Mà AC = BD (do ABCD là hình thang cân) nên $\stackrel{⌢}{AC}=\stackrel{⌢}{BD}$. Do đó $\widehat{EAC}=\widehat{xDB}$ .

Vậy tứ giác AEDM nội tiếp được trong một đường tròn.

2. Chứng minh AB // EM

Tứ giác AEDM nội tiếp nên $\widehat{EAD}=\widehat{EMD}$ (cùng chắn cung ED). Mà $\widehat{EAD}=\widehat{ABD}$ (góc tạo bởi tia tiếp tuyến và dây cung với góc nội tiếp cùng chắn cung AD).

Suy ra: $\widehat{EMD}=\widehat{ABD}$ . Do đó EM // AB.

3. Chứng minh M là trung điểm HK

ΔDAB có HM // AB $\Rightarrow \frac{HM}{AB}=\frac{DH}{DA}$ .

ΔCAB có MK // AB $\Rightarrow \frac{MK}{AB}=\frac{CK}{CB}$ .

Mà $\frac{DH}{DA}=\frac{CK}{CB}$ (định lí Ta let cho hình thang ABCD).

Nên $\frac{HM}{AB}=\frac{MK}{AB}$ .

Do đó MH = MK.

Vậy M là trung điểm HK.

4. Chứng minh $\frac{2}{HK}=\frac{1}{AB}+\frac{1}{CD}$ .

Áp dụng hệ quả định lí Ta let cho  tam giác ADB  có HM // AB ta được:

$\frac{HM}{AB}=\frac{DM}{DB}$ (1).

Áp dụng hệ quả định lí Ta let cho  tam giác BCD  có KM // CD ta được: $\frac{KM}{CD}=\frac{BM}{BD}$ (2).

Cộng (1) và (2) vế theo vế ta được:

$\frac{HM}{AB}+\frac{KM}{CD}=\frac{DM}{DB}+\frac{BM}{BD}=\frac{DM+BM}{BD}=\frac{BD}{BD}=1$

Suy ra: $\frac{2HM}{AB}+\frac{2KM}{CD}=2$ ,

mà MH = MK nên 2HM = 2KM = HK.

Do đó: $\frac{HK}{AB}+\frac{HK}{CD}=2$ .

Suy ra: $\frac{2}{HK}=\frac{1}{AB}+\frac{1}{CD}$ (đpcm).

Lời bàn:

1. Do AC = BD $\Rightarrow \stackrel{⌢}{ADC}=\stackrel{⌢}{BCD}$ nên để chứng minh tứ giác AEDM nội tiếp ta sử dụng phương pháp: Nếu tứ giác có góc ngoài tại một đỉnh bằng góc đối của đỉnh của đỉnh đó thì tứ giác đó nội tiếp. Với cách suy nghĩ trên chỉ cần vẽ tia Dx là tia đối của tia tiếp tuyến DE thì bài toán giải quyết được dễ dàng. Có thể chứng minh tứ giác AEDM nội tiếp bằng cách chứng minh khác được không? (phần này dành cho các em suy nghĩ nhé)

2. Câu 3 có còn cách chứng minh nào khác không? Có đấy. Thử chứng minh tam giác AHM và tam giác BKM bằng nhau từ đó suy ra đpcm.

3. Câu 4 là bài toán quen thuộc ở lớp 8 phải không các em? Do đó khi học toán các em cần chú ý các bài tập quen thuộc nhé. Tuy vậy câu này vẫn còn một cách giải nữa đó. Em thử nghĩ xem?