- Nhắc lại định nghĩa, tính chất cơ bản của bất đẳng thức
- Phương pháp chứng minh bất đẳng thức bằng định nghĩa
- Chứng minh bất đẳng thức bằng phương pháp biến đổi tương đương
- Áp dụng bất đẳng thức để chứng minh bất đẳng thức
- Chứng minh bất đẳng thức bằng phương pháp phản chứng
- Chứng minh bất đẳng thức bằng phương pháp làm trội, làm giảm
- Một số loại bài chứng minh bất đẳng thức thường gặp
- Mở rộng một số bất đẳng thức
- Ứng dụng của bất đẳng thức trong Toán THCS
- Một số bài tập bất đẳng thức
- Phương pháp đổi biến chứng minh bất đẳng thức
- Một số ví dụ chứng minh BĐT bằng phương pháp cân bằng hệ số
- Kỹ thuật chọn điểm rơi chứng minh bất đẳng thức
- Một số ví dụ chứng minh BĐT bằng phương pháp hệ số bất định UCT
- Một số ví dụ chứng minh BĐT bằng phương pháp Cauchy ngược dấu
Chúng ta có thể sử dụng các bất đẳng thức đã biết vào các bài toán chứng minh bất đẳng thức như: Cosi, Bunhiacopxki,…và các BĐT luôn đúng.
Toancap2.net liệt kê ra các bất đẳng thức đã biết, đã được chứng minh và các em có thể áp dụng ngay vào giải toán mà không cần phải chứng minh lại. Cụ thể là:
Mục lục [hiện]
1. BĐT bình phương của một biểu thức
A2 ≥ 0 với mọi giá trị của A.
Dấu “=” xảy ra khi và chỉ khi A = 0
2. Bất đẳng thức Côsi
(Cauchy là tên của Nhà toán học người Pháp 1789 – 1857)
+ Cho hai số a và b không âm , ta luôn có:
Dấu “=” xảy ra khi và chỉ khi a = b
+ Cho ba số a, b, c không âm , ta luôn có:
Dấu “=” xảy ra khi và chỉ khi a = b = c
+ Tổng quát:
Cho n số a1, a2 ,…, an không âm, ta luôn có:
Dấu “=” xảy ra khi và chỉ khi a1 = a2 = …=an
(Trung bình cộng của n số không âm không nhỏ hơn trung bình nhân của chúng)
3. Bất đẳng thức Bunhiacốpxki
(Bunhiacôpxki là tên của Nhà toán học người Nga 1804 – 1889)
+ Cho các số a1,a2; b1, b2 ta có: (a1b1 + a2.b2)2 ≤ (a12 + a22) (b12 + b22)
Dấu “=” xảy ra khi và chỉ khi
+ Tổng quát: Cho hai bộ số (a1, a2,…an) và (b1, b2, …bn) ta luôn có :
Dấu “=” xảy ra khi và chỉ khi:
(Bình phương của tổng các tích không lớn hơn tích của tổng các bình phương)
3. BĐT tổng nghịch đảo của hai số cùng dấu
Với hai số cùng dấu a và b ta có:
* BĐT. với a và b là hai số dương.
Dấu “=” xảy ra khi và chỉ khi a = b
* Ngoài ra: BĐT
Dấu “=” xảy ra khi và chỉ khi a = b
Với việc áp dụng các bất đẳng thức trên, Để chứng minh A > B ta tiến hành như sau:
– Từ BĐT đã biết C > D ta đi biến đổi C > D ⇒ …..⇒ A > B rồi trả lời.
các em xem những ví dụ dưới đây để hiểu rõ hơn về cách sử dụng các bất đẳng thức đã biết ở trên để chứng minh bất đẳng thức.
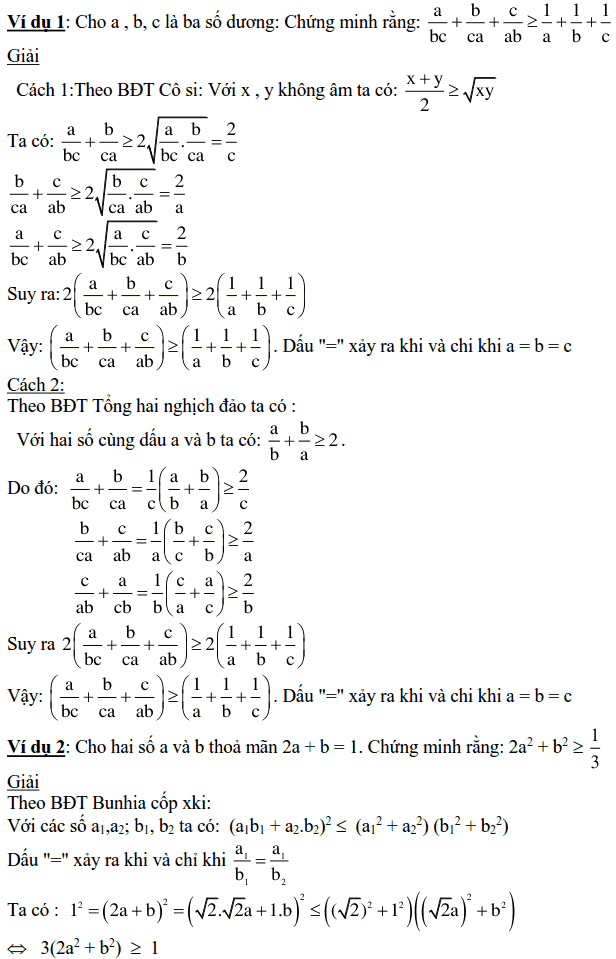

Bài viết liên quan
- Cách giải bài toán BĐT và tìm GTNN, GTLN trong đề thi vào 10 môn Toán
- Một số ví dụ chứng minh BĐT bằng phương pháp ghép cặp
- Một số ví dụ chứng minh BĐT bằng phương pháp Cauchy ngược dấu
- Một số ví dụ chứng minh BĐT bằng phương pháp hệ số bất định UCT
- Một số ví dụ chứng minh BĐT bằng phương pháp cân bằng hệ số