Bài 3: Cho nửa đường tròn (O) đường kính AB = a. Gọi Ax, By là các tia vuông góc với AB ( Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (O) (M khác A và B) kẻ tiếp tuyến với nửa đường tròn (O); nó cắt Ax, By lần lượt ở E và F.
1. Chứng minh: $ \widehat{\text{EOF}}={{90}^{0}}$
2. Chứng minh tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.
3. Gọi K là giao điểm của AF và BE, chứng minh MK ⊥ AB.
4. Khi MB = $ \sqrt{3}$ .MA, tính diện tích tam giác KAB theo a.
BÀI GIẢI CHI TIẾT:
1. Chứng minh: $ \widehat{\text{EOF}}={{90}^{0}}$ .
EA, EM là hai tiếp tuyến của đường tròn (O) cắt nhau ở E nên OE là phân giác của $ \widehat{AOM}$.
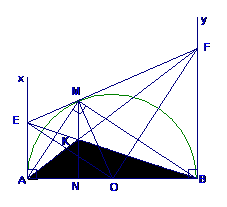
hình 4
Tương tự: OF là phân giác của $ \widehat{BOM}$ .
Mà $ \widehat{AOM}$ và $ \widehat{BOM}$ kề bù nên: $ \widehat{EOF}={{90}^{0}}$ (đpcm)
2. Chứng minh: Tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.
Ta có: $ \widehat{EAO}=\widehat{EMO}={{90}^{0}}$ (tính chất tiếp tuyến)
Tứ giác AEMO có $ \widehat{EAO}+\widehat{EMO}={{180}^{0}}$ nên nội tiếp được trong một đường tròn.
Tam giác AMB và tam giác EOF có: $ \widehat{AMB}=\widehat{\text{EOF}}={{90}^{0}}$ , $ \widehat{MAB}=\widehat{MEO}$ (cùng chắn cung MO của đường tròn ngoại tiếp tứ giác AEMO. Vậy Tam giác AMB và tam giác EOF đồng dạng (g.g).
3. Gọi K là giao điểm của AF và BE, chứng minh MK ⊥ AB
Tam giác AEK có AE // FB nên: $ \frac{AK}{KF}=\frac{AE}{BF}$ . Mà : AE = ME và BF = MF (t/chất hai tiếp tuyến cắt nhau). Nên $ \frac{AK}{KF}=\frac{ME}{MF}$ . Do đó MK // AE (định lí đảo của định lí Ta- let). Lại có: AE ⊥ AB (gt) nên MK ⊥ AB.
4. Khi MB = $ \sqrt{3}$ .MA, tính diện tích tam giác KAB theo a.
Gọi N là giao điểm của MK và AB, suy ra MN ⊥ AB.
ΔFEA có MK//AE nên $ \frac{MK}{AE}=\frac{FK}{FA}$ (1). ΔBEA có NK//AE nên $ \frac{NK}{AE}=\frac{BK}{BE}$ (2).
Mà $ \frac{FK}{KA}=\frac{BK}{KE}$ (do BF // AE) nên $ \frac{FK}{KA+FK}=\frac{BK}{BK+KE}$ hay $ \frac{FK}{FA}=\frac{BK}{BE}$ (3).
Từ (1), (2) và (3) suy ra $ \frac{MK}{AE}=\frac{KN}{AE}$ . Vậy MK = NK.
Tam giác AKB và tam giác AMB có chung đáy AB nên: $ \frac{{{S}_{AKB}}}{{{S}_{AMB}}}=\frac{KN}{MN}=\frac{1}{2}$ .
Do đó: $ {{S}_{AKB}}=\frac{1}{2}{{S}_{AMB}}$
Tam giác AMB vuông ở M nên tan A = $ \frac{MB}{MA}=\sqrt{3}$ ⇒ $ \widehat{MAB}={{60}^{0}}$ .
Vậy AM = $ \frac{a}{2}$ và MB = $ \frac{a\sqrt{3}}{2}$
⇒ $ {{S}_{AKB}}=\frac{1}{2}.\frac{1}{2}.\frac{a}{2}.\frac{a\sqrt{3}}{2}$ = $ \frac{1}{16}{{a}^{2}}\sqrt{3}$ (đvdt).
Lời bàn:
(Đây là đề thi tuyển sinh vào lớp 10 năm học 2009-2010 của tỉnh Hà Nam) .
Từ câu 1 đến câu 3 trong quá trình ôn thi vào lớp 10 chắc chắn thầy cô nào cũng ôn tập, do đó những em nào ôn thi nghiêm túc chắc chắn giải được ngay, khỏi phải bàn, những em thi năm qua ở tỉnh Hà Nam xem như trúng tủ. Bài toán này có nhiều câu khó, và đây là một câu khó mà người ra đề khai thác từ câu: MK cắt AB ở N. Chứng minh: K là trung điểm MN.
Nếu chú ý MK là đường thẳng chứa đường cao của tam giác AMB do câu 3 và tam giác AKB và AMB có chung đáy AB thì các em sẽ nghĩ ngay đến định lí: Nếu hai tam giác có chung đáy thì tỉ số diện tích hai tam giác bằng tỉ số hai đường cao tương ứng, bài toán qui về tính diện tích tam giác AMB không phải là khó phải không các em?