Đề cương ôn tập Hình học 7 chương 1 THCS Giảng Võ 2018-2019

Đề cương ôn tập Hình học 7 chương 1 trường THCS Giảng Võ, quận Ba Đình, TP Hà Nội, năm học 2018-2019.

Có các dạng bài tập: Vẽ hình, Tính số đo góc và Nhận biết hai đường thẳng song song, hai đường thẳng vuông góc.

Dạng 1. Bài tập vẽ hình

Bài 1: Vẽ hình theo cách diễn đạt sau

– Vẽ góc MON có số đo bằng $ {{70}^{o}}$. Lấy điểm I bất kỳ nằm trong góc MON

– Vẽ qua điểm I, đường thẳng d vuông góc với OM và đường thẳng a song song với ON.

Bài 2: Vẽ hình theo yêu cầu sau:

– Vẽ $ \Delta MNP$ có $ \widehat{M}={{90}^{o}}$

– Quan N kẻ tia Nt // MP (tia Nt thuộc nửa mặt phẳng bờ là đường thẳng MN không chứa điểm P)

– Vẽ tia phân giác Px của $ \widehat{{NPM}}$ cắt MN tại I, cắt Nt tại H

– Vẽ $ MK\bot PI$

– Vẽ đường thẳng d là đường trung trực của đoạn thẳng HN.

Bài 3: Vẽ hình theo yêu cầu sau:

– Vẽ $ \Delta ABC$ có $ \displaystyle \widehat{A}={{90}^{o}}$ (AB > AC)

– Vẽ tia phân giác AI của góc A cắt BC tại I

– Vẽ $ BE\bot AI,CF\bot AI(E,F\in AI)$

– Qua B kẻ tia Bt // AC (tia Bt thuộc nửa mặt phẳng bờ là đường thẳng AB chứa điểm C)

Bài 4: Vẽ $ \Delta ABC$ biết $ \widehat{B}={{105}^{o}};\widehat{C}={{35}^{o}}$

– Trên nửa mặt phẳng bờ là đường thẳng AB chứa điểm C, vẽ tia Ax sao cho Ax // BC

– Kẻ $ AH\bot BC(H\in BC)$

– Qua A kẻ tia $ Ay\bot AH$(Ay thuộc nửa mặt phẳng bờ là đường thẳng AB không chứa điểm C)

– Vẽ đường thẳng d là đường trung trực của đoạn thẳng AH.

Bài 5:

a) Vẽ góc xOy có số đo bằng $ {{85}^{o}}$

b) Vẽ góc mOt đối đỉnh với góc xOy

c) Tính số đo các góc còn lại?

Bài 6:

a) Vẽ hình theo diễn đạt bằng lời sau:

– Vẽ tam giác ABC

– Vẽ đường thẳng d đi qua A và song song với BC.

– Vẽ đường thẳng a là đường trung trực của đoạn thẳng BC.

b) Hỏi $ d\bot a$ không? Vì sao?

Dạng 2: Tính số đo góc

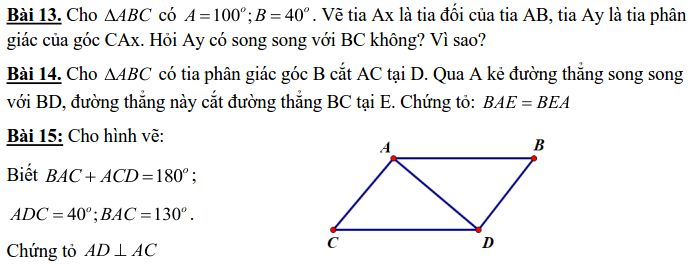
Bài 7. Tìm số đo x, y, z trong mỗi hình sau:

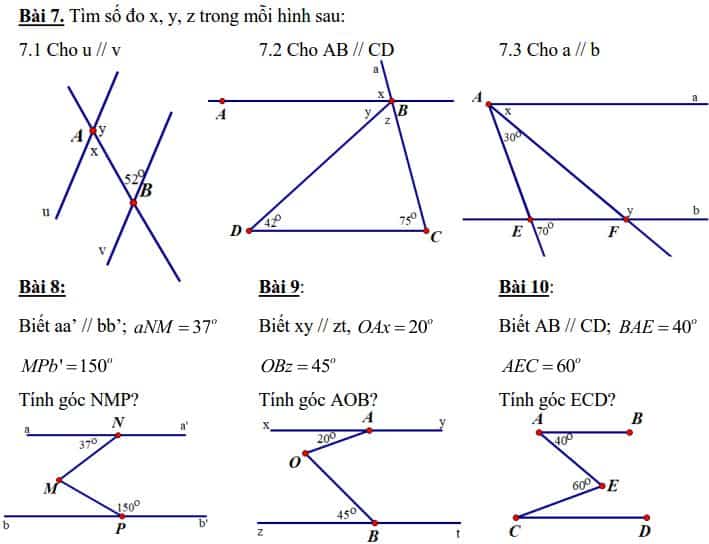
Dạng 3: Nhận biết hai đường thẳng song song, hai đường thẳng vuông góc

Bài 16. Cho góc xOy nhọn. Lấy điểm A thuộc tia Ox. Trong góc xOy vẽ tia Am song song với Oy. Gọi Ot, An lần lượt là tia phân giác của góc xOy và góc xAn

a) Chứng minh: An // Ot

b) Vẽ tia Az là tia phân giác của góc OAm. Chứng minh $ Az\bot An$

c) Chứng minh $ Az\bot Ot$

Bài 17. Cho $ \Delta ABC$, Ax là tia phân giác BAC. Từ C kẻ đường thẳng song song với tia Ax, cắt tia đối của tia AB tại D.

a) Chứng minh $ \widehat{{xAB}}=\widehat{{ADC}}=\widehat{{ACD}}$

b) Kẻ tia Ay là tia phân giác của góc DAC. Chứng minh $ \widehat{{xAy}}={{90}^{o}}$

c) Chứng minh : $ Ay\bot CD$

d) Trên nửa mặt phẳng bờ AD không chứa điểm C, vẽ tia Az sao cho $ \widehat{{zAD}}=\widehat{{ADC}}$. Chứng minh $ \widehat{{zAx}}={{180}^{o}}$

Bài 18. Cho $ \Delta ABC$ có $ \widehat{A}={{90}^{o}}$. Qua B kẻ tia BM // AC (tia BM thuộc nửa mặt phẳng bờ là đường thẳng AB có chứa điểm C)

a) Chứng minh $ BM\bot AB$

b) Trên cùng một nửa mặt phẳng bờ BC có chứa điểm A, vẽ về phía ngoài $ \Delta ABC$ hai tia Bx và tia Cy sao cho $ \widehat{{xBA}}=\widehat{{yCA}}={{45}^{o}}$. Chứng tỏ Bx // Cy

c) Vẽ tia BN sao cho Bx là tia phân giác của NBA. Chứng minh 3 điểm B, M, N thẳng hàng.