Đề thi HK2 môn Toán 9 quận Tân Bình năm 2018-2019

Đề thi học kì 2 môn Toán lớp 9 quận Tân Bình, TP Hồ Chí Minh năm học 2018-2019. Thời gian làm bài: 90 phút.

Câu 1: (1,5 điểm) Giải các phương trình sau

a) $ {{x}^{2}}-(2+\sqrt{3})x+2\sqrt{3}=0$

b) x⁴ + 8x² =9

Câu 2: (1,5 điểm) Trong mặt phẳng tọa độ Oxy cho hàm số $ y=-\frac{1}{4}$ x² có đồ thị (P).

a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy

b) Cho đường thẳng (d): y= -2x +3. Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.

Bài 3: (1 điểm) cho phương trình x² – (m+1)x +2m-3=0 (1) với x là ẩn số, m là tham số.

a) Chứng minh (1) luôn có hai nghiệm phân biệt với mọi giá trị của m.

b) Gọi x₁, x₂ là hai nghiệm của (1). Tìm m để $ \left( {{{x}_{1}}^{2}+{{x}_{2}}^{2}} \right)+{{x}_{1}}{{x}_{2}}=8$

Bài 4: (1 điểm) Hai máy photo cùng photo một lượng đề kiểm tra học kì 2 mất 12 ngày. Nếu máy photo thứ nhất photo trong 4 ngày và máy photo thứ hai photo trong 10 ngày thì chỉ hoàn thành được $ \frac{2}{3}$ lượng đề kiểm tra. Hỏi nếu làm riêng thì mỗi máy photo hoàn thành lượng đề kiểm tra đó trong bao lâu? ( Biết thời gian 3 máy photo mỗi ngày là như nhau).

Bài 5: (1 điểm) Chủ nhật tuần qua, Bố bạn An có tổ chức cho gia đình về quê bằng ô tô từ Thành phố Hồ chí minh đi Long An cách 60km với vận tốc dự định trước. Nhưng sau khi đi được $ \frac{1}{3}$ quãng đường, Bố bạn An tăng vận tốc thêm 10km/h trên quãng đường còn lại nên đến Long An sớm hơn dự định 8 phút. Hỏi thời gian bố Bạn AN dự định đi từ Thành phố Hồ chí minh đến Long An là bao nhiêu giờ?

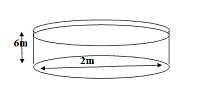
Bài 6: (1 điểm) Bác Hùng có xây một hồ cá hình trụ, đáy của hồ là một hình tròn có đường kính 2m, người ta đo được mực nước có trong hồ cao 0,6m.

a) Tính thể tích nước có trong hồ.

b) Người ta bỏ một số lượng sỏi đá vào hồ, làm mực nước trong hồ dâng cao thêm 0,1m. Hỏi thể tích lượng sỏi đá trong hồ chiếm bao nhiêu?

(Thể tích hình trụ $ V=\pi {{R}^{2}}h;\pi =3,14$ ;R là bán kính đáy, h là chiều cao hình trụ. Kết quả làm tròn 1 chữ số thập phân).

Bài 7: (3 điểm) Cho tam giác ABC nhọn, AB<AC. Vẽ đường tròn (O) đường kính BC cắt hai cạnh AB,AC lần lượt tại E,D ; BD cắt CE tại H, AH cắt BC tại F.

a) Chứng minh AF vuông góc với BC tại F và tứ giác BEHF nội tiếp

b) Tia DE cắt đường thẳng BC tại S. Chứng minh SE.SD=SB.BC

c) Tia AH cắt (O) tại K(F nằm giữa A và K). Chứng minh SK là tiếp tuyến của (O).