Phòng giáo dục và đào tạo huyện Yên Định, đề thi học sinh giỏi cấp huyện năm học 2012 – 2013, môn thi Toán 9.
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1: (3 điểm) Cho A =
a) Rút gọn A.
b) Tìm x để A > 0 .
c) Tìm giá trị lớn nhất của A .
Câu 2: (6 điểm)
a) Giải phương trình:
b) Giải bất phương trình: |2x-7| < x2 + 2x + 2
c) Giải hệ phương trình:
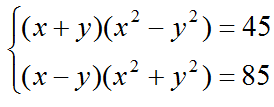
Câu 3 : (4 điểm)
a) Cho a + b +c = 0, tính giá trị của biểu thức:
b) Tìm số tự nhiên n sao cho là số A = n2 + n + 6 chính phương.
Câu 4 : (5 điểm)
a) Từ một điểm A nằm ngoài (O;R) kẻ hai tiếp tuyến AM, AN (M,N(O;R)). Trên cung nhỏ MN lấy điểm P khác M và Tiếp tuyến tại P cắt AM tại B, cắt AN tại C. Cho A cố định và AO = a. Chứng minh chu vi tam giác ABC không đổi khi P di động trên cung nhỏ MN. Tính giá trị không đổi ấy theo a và R.
b) Cho tam giác ABC có diện tích bằng 36 (đơn vị diện tích). Trên cạnh BC và cạnh CA lần lượt lấy điểm D và E sao cho DC = 3DB và EA = 2EC; AD cắt BE tại I. Tính diện tích tam giác BID.
Câu 5: (2 điểm) Tìm giá trị nhỏ nhất của biểu thức:
Tải file pdf Đề thi học sinh giỏi Toán 9 huyện Yên Định 2012-2013