Đề thi giải Toán trên máy tính Casio khối 9 huyện Cái Bè

KỲ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN GIẢI TOÁN TRÊN MÁY TÍNH CASIO KHỐI 9 THCS

(Năm học 2012 – 2013)

Thời gian làm bài: 120 phút – Ngày thi: 06/11/2012

Quy định: 1/ Thí sinh làm bài trên mẫu giấy thi do Hội đồng coi thi phát.

                 2/ Thí sinh chú ý:  làm bài  theo hướng dẫn của từng bài.

                3/ Thí sinh được sử dụng các loại máy sau đây: Casio fx- 500MS, ES; Casio fx- 570MS,ES PLUS; Casio fx 500 VNPLUS;; Vinacal Vn- 500 MS, 570MS và  vinacal- 570MS New

               4/ Đề thi có 06 bài, mỗi bài 5,0 điểm, Đề gồm 2 trang

Bài 1: (5 điểm) : (yêu cầu tóm tắt cách giải và nêu ra kết quả)

Câu 1: Tính giá trị của  biểu thức:

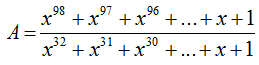
Khi x = 2

Câu 2: Rút gọn:

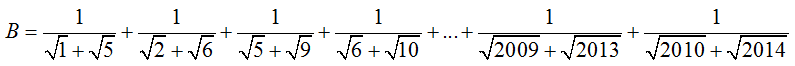
(kết quả làm tròn đến 4 chữ số thập phân)

Bài 2: ( 5 điểm):

Cho ba hàm số số y = $ \displaystyle \frac{8}{7}x-2$ ( 1), y = $ \displaystyle \frac{3}{8}x-3$ (2) , y = -$ \displaystyle \frac{18}{29}x+6$ (3)

1/ Vẽ đồ thị của ba hàm số trên mặt phẳng toạ độ Oxy

2/Tìm toạ độ giao điểm A ( x_A, y_A) của hai đồ thị hàm số ( 1) và ( 2); giao điểm B( x_B, y_B) của hai đồ thị hàm số (2 ) và ( 3); giao điểm của C( x_C, y_C) của hai đồ thị hàm số ( 1) và ( 3) ( kết quả dưới dạng phân số hoặc hỗn số)

3/ Tính các góc của tam giác ABC ( Lấy nguyên kết quả trên máy)

Bài 3:( 5 điểm)

Câu 1: Cho một hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại điểm O, đường trung trực d của đoạn thẳng AB tại điểm H cắt BD tại điểm M và cắt AC tại điểm N. Biết NA = a, MB = b. Tính diện tích S của hình thoi ABCD khi a = 2603,1931cm, b = 26032,012cm.

Câu 2: Mảnh đất phẳng có dạng hình thang cân và chiều dài hai đáy là 40m và 100m còn chiều cao của hình thang là 35m. Tính độ dài cạnh bên mảnh đất.

Bài 4:( 5 điểm)

Câu 1: Tìm số tự nhiên n để u_n nhỏ nhất

u_n  = n + $ \displaystyle \frac{2012}{{{n}^{3}}}$ với n ∈ N

Câu 2: Cho dãy số $ \displaystyle \left\{ {{U}_{n}} \right\}$ với n là số tự nhiên khác 0, có U₁ = 1, U₂ = 2, U₃ = 3 và U_n+3 = 2U_n-2 – 3U_n+1 + 2U_n.

a) Viết quy trình bấm máy để tính U_{n+ 3} rối tính U₁₉ , U₂₀ , U₆₆ , U₆₇ , U₆₈

b) Viết quy trình bấm máy để tính tổng của 20 hạng đầu tiên của dãy số đó.

Bài 5:( 5 điểm) ( Yêu cầu chỉ  nêu kết quả)

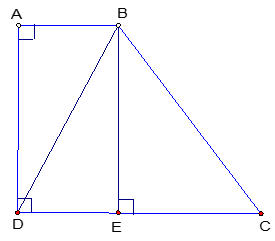
Cho hình thang vuông ABCD ( hình vẽ ). Biết AB = 2,25cm, góc ABD = 50⁰, diện tích hình thang ABCD là  9,92cm². Tính độ dài các cạnh AD, DC, BC và số đo góc ABC, góc BCD?

Bài 6: ( 5 điểm)

Câu 1: Giải hệ phương trình (Yêu cầu chỉ nêu kết quả và lấy đủ các chữ số thập phân trên máy tính)

$ \displaystyle \left\{ \begin{array}{l}2,518x-84,26y=4,6821\\19,26x+6,571y=-2,843\end{array} \right.$

Câu 2: Tìm x, y nguyên dương, x ≥ 1 thỏa mãn: y = $ \displaystyle \sqrt[3]{9+\sqrt{x-1}}+\sqrt[3]{9-\sqrt{x-1}}$

——————————————— Hết——————————————————

Ghi chú: Giám thị không giải thích gì thêm