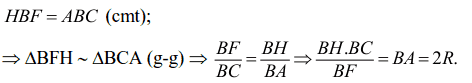Đề thi vào lớp 10 môn Toán Sở giáo dục và đào tạo tỉnh Quảng Ninh năm học 2018 -2019. Thời gian làm bài 120 phút, không kể thời gian giao đề. Có đáp án.
Nội dung đề thi:
Câu 1. (2,5 điểm)
- Thực hiện phép tính: $ \displaystyle \frac{\sqrt{27}}{\sqrt{3}}$
- Rút gọn biểu thức: P = $ \displaystyle \left( \frac{\sqrt{x}}{3 \sqrt{x}} \frac{9 x}{9-x} \right).\left( 3\sqrt{x}-x \right)$ với x ≥ 0 và x ≠ 9.
- Xác định các hệ số a, b để đồ thị của hàm số y = ax b đi qua hai điểm A(2; –2) và B(–3; 2)
Câu 2. (1,5 điểm)
- Giải phương trình: x2 – 4x 4 = 0
- Tìm giá trị của m để phương trình x2 – 2(m 1)x m2 3 = 0 có hai nghiệm x1, x2 thỏa mãn |x1| |x2| = 10
Câu 3. (1,5 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156 km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36 km so với lúc đi và vận tốc tăng so với lúc đi là 32 km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.
Câu 4. (3,5 điểm)
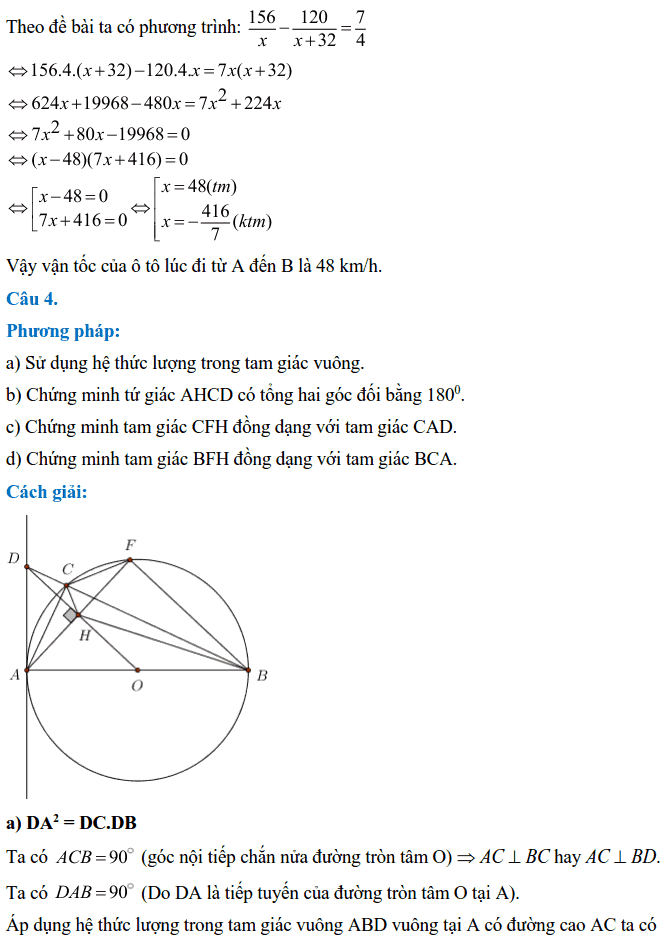
Cho đường tròn tâm O, đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A và B). Tiếp tuyến của đường tròn (O) tại A cắt tia BC ở điểm D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm F (không trùng với A). Chứng minh:
a. DA2 = DC.DB
b. Tứ giác AHCD nội tiếp
c. CH ⊥ CF
d. $ \displaystyle \frac{\text{BH}\text{.BC}}{\text{BF}}\text{ = 2R}$
Câu 5. (0,5 điểm) Cho x, y là các số thực dương thỏa mãn: xy 1 ≤ x. Tìm giá trị lớn nhất của biểu thức: Q = $ \displaystyle \frac{x y}{\sqrt{3{{x}^{2}}-xy {{y}^{2}}}}$
Hướng dẫn giải:
