Đề thi học kì 2 môn Toán lớp 9 quận Thanh Xuân, Hà Nội năm học 2018-2019. Thời gian làm bài: 90 phút. Có lời giải.
Bài 1 (2 điểm). Cho hai biểu thức A = $ \frac{{\sqrt{x}+8}}{{x+7}}$ và
B = $ \frac{{\sqrt{x}}}{{\sqrt{x}-3}}+\frac{{8\sqrt{x}+24}}{{x-9}}$ với x ≥ 0; x ≠ 9
1) Tính giá trị của biểu thức A khi x = 25
2) Chứng minh $ B=\frac{{\sqrt{x}+8}}{{\sqrt{x}-3}}$
3) Tìm GTNN của P=$ \sqrt{{\frac{B}{A}}}$
Bài 2 (2 điểm). Giải toán bằng cách lập phương trình hoặc hệ phương trình
Đội sản xuất phải làm 1.000 sản phẩm trong thời gian quy định .Nhờ tăng năng suất lao động, nên mỗi ngày đội làm thêm được 30 sản phẩm so với kế hoạch. Vì vậy chẳng những đã làm vượt mức kế hoạch 170 sản phẩm mà còn hoàn thành công việc sớm hơn dự định một ngày. Tính số sản phẩm mà đội sản xuất phải làm trong một ngày theo kế hoạch.
Bài 3 (2 điểm).
1) Giải hệ phương trình: $ \left\{ \begin{array}{l}\sqrt{{3-x}}+\frac{2}{{\sqrt{{y-2}}}}=5\\4\sqrt{{3-x}}+\frac{3}{{\sqrt{{y-2}}}}=15\end{array} \right.$
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng d: y= 6x +m2 -1 với m là tham số và parabol (P): y=x2
a) Chứng minh d luôn cắt (P) tại hai điêm phân biệt với mọi số thực m
b) Gọi x1, x2 là hoành độ giao điểm của d và (P). Tìm m để x12 – 6x2 +x1x2=48
Bài 4 (3,5 điểm)
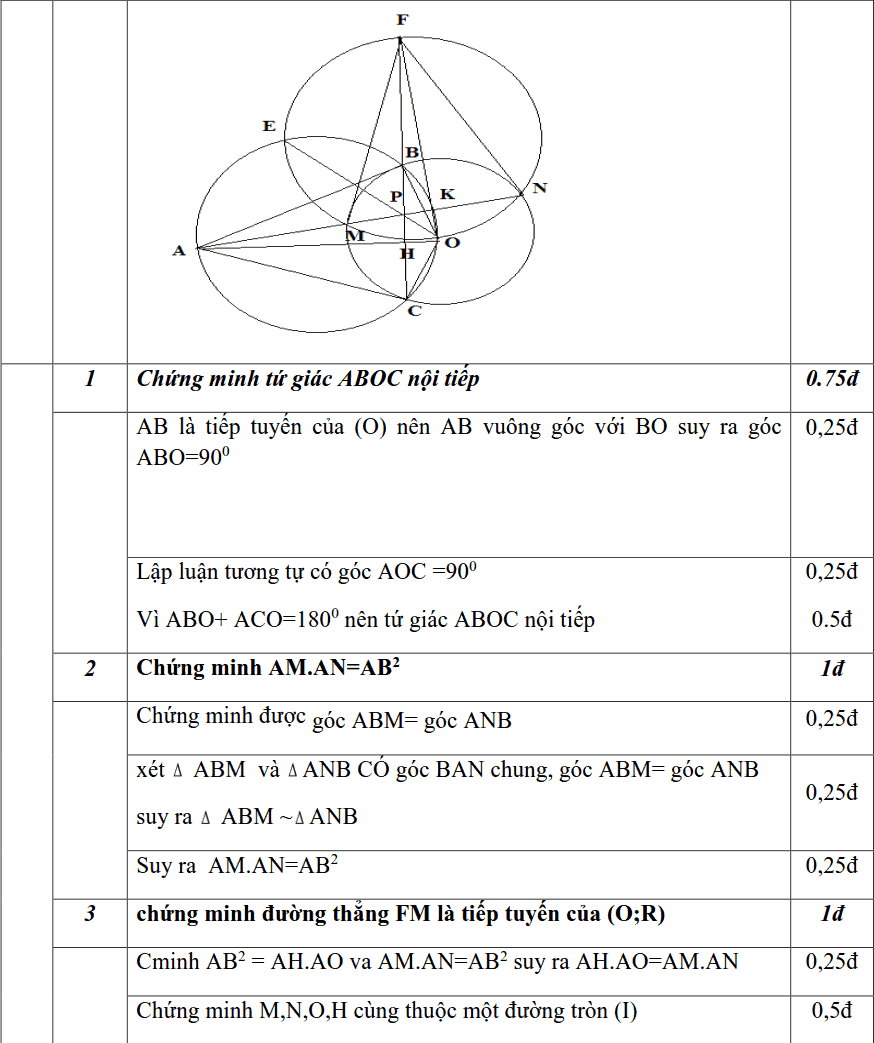
Cho điểm A nằm ngoài đường tròn (O;R). từ điểm A vẽ các tiếp tuyến AB,AC với B,C là tiếp điểm, và cát tuyến AMN với đường tròn (O). ( với MN không đi qua tâm và AM<AN).
1) Chứng minh tứ giác ABOC nội tiếp
2) Chứng minh AM.AN=AB2
3) Tiếp tuyến tại N của (O) cắt đường thẳng BC tại điểm F. chứng minh đường thẳng FM là tiếp tuyến của (O;R)
4) Gọi P là giao điểm của dây BC và dây MN, E là giao điểm của đường tròn ngoại tiếp tam giác MNO và đường tròn ngoại tiếp tứ giác ABOC ( E khác O).
Chứng minh P,E,O thẳng hàng
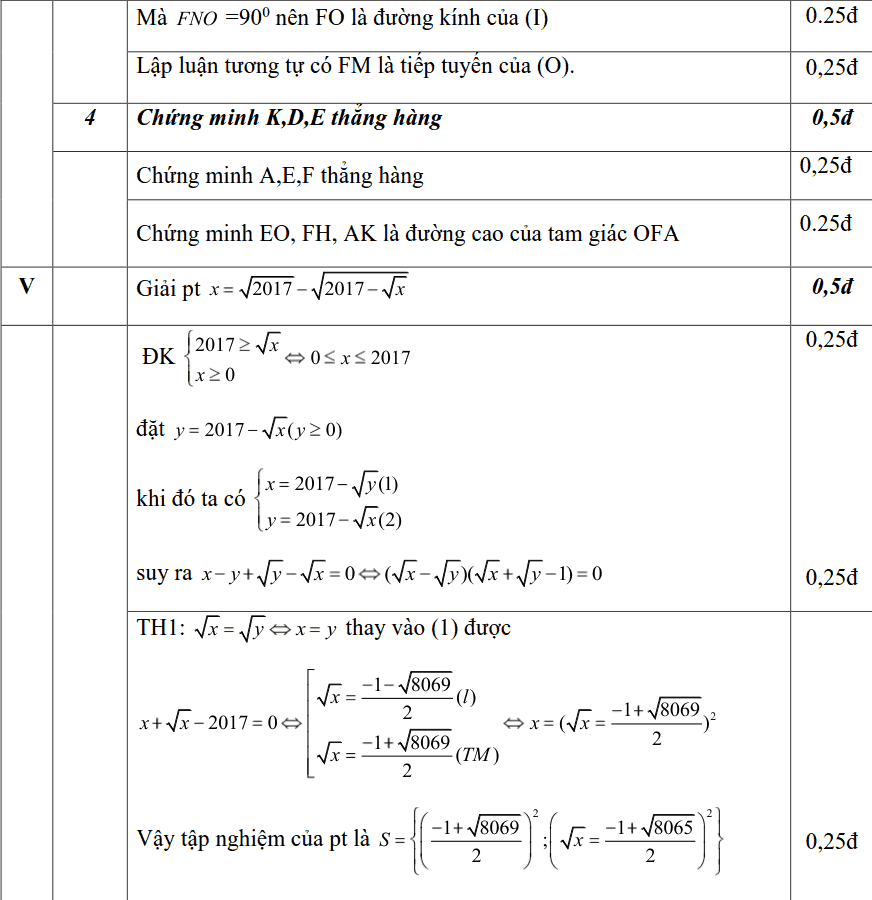
Bài 5 (0,5 điểm). giải phương trình $ x=\sqrt{{2017}}-\sqrt{{2017-\sqrt{x}}}$
Hướng dẫn giải đề kiểm tra HK2 môn Toán 9 quận Thanh Xuân năm 2018-2019:
