Đề thi Toán vào lớp 10 TP. Hồ Chí Minh năm học 2014-2015

Đề thi tuyển sinh vào lớp 10 môn Toán TP. Hồ Chí Minh năm học 2014-2015

Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Bài 1: (2 điểm)

Giải các phương trình và hệ phương trình sau:

a) ${\displaystyle x^2-7x+12=0}$

b) ${\displaystyle x^2-(\sqrt{2}+1)x+\sqrt{2}=0}$

c) ${\displaystyle x^4-9x^2+20=0}$

d) ${\displaystyle \{\begin{array}{c}3x-2y=4\\ 4x-3y=5\end{array}}$

Bài 2: (1,5 điểm)

a) Vẽ đồ thị (P) của hàm số và đường thẳng (D):  trên cùng một hệ trục toạ độ.

b) Tìm toạ độ các giao điểm của (P) và (D) ở câu trên bằng phép tính.

Bài 3: (1,5 điểm)

Thu gọn các biểu thức sau:

${\displaystyle A=\frac{5+\sqrt{5}}{\sqrt{5}+2}+\frac{\sqrt{5}}{\sqrt{5}-1}-\frac{3\sqrt{5}}{3+\sqrt{5}}}$

${\displaystyle B=(\frac{x}{x+3\sqrt{x}}+\frac{1}{\sqrt{x}+3}):(1-\frac{2}{\sqrt{x}}+\frac{6}{x+3\sqrt{x}})}$ (x > 0)

Bài 4: (1,5 điểm)

Cho phương trình ${\displaystyle x^2-mx-1=0}$ (1) (x là ẩn số)

1. a) Chứng minh phương trình (1) luôn có 2 nghiệm trái dấu
2. b) Gọi x₁, x₂ là các nghiệm của phương trình (1):

Tính giá trị của biểu thức:

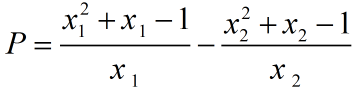
Bài 5: (3,5 điểm)

Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O (AB < AC). Các đường cao AD và CF của tam giác ABC cắt nhau tại H.

a) Chứng minh tứ giác BFHD nội tiếp. Suy ra ${\displaystyle \widehat{AHC}={180}^0-\widehat{ABC}}$

b) Gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C) và N là điểm đối xứng của M qua AC. Chứng minh tứ giác AHCN nội tiếp.

c) Gọi I là giao điểm của AM và HC; J là giao điểm của AC và HN. Chứng minh ${\displaystyle \widehat{AJI}=\widehat{ANC}}$

d) Chứng minh rằng : OA vuông góc với IJ

Gợi ý giải:

Bài 1: (2 điểm)

Giải các phương trình và hệ phương trình sau:

a) ${\displaystyle x^2-7x+12=0}$

${\displaystyle \mathrm{\Delta }=7^2-4.12=1}$

${\displaystyle \iff x=\frac{7+1}{2}=4hayx=\frac{7-1}{2}=3}$

b) ${\displaystyle x^2-(\sqrt{2}+1)x+\sqrt{2}=0}$

Phương trình có : a + b + c = 0 nên có 2 nghiệm là: ${\displaystyle x=1hayx=\frac{c}{a}=\sqrt{2}}$

c) ${\displaystyle x^4-9x^2+20=0}$

Đặt u = x² ≥ 0 pt thành: ${\displaystyle u^2-9u+20=0\iff (u-4)(u-5)=0}$

${\displaystyle \iff u=4hayu=5}$

Do đó pt ${\displaystyle \iff x^2=4hay{x}^2=5\iff x=\pm 2hayx=\pm \sqrt{5}}$

d) ${\displaystyle \{\begin{array}{c}3x-2y=4\\ 4x-3y=5\end{array}}$

⇔ ${\displaystyle \{\begin{array}{c}12x-8y=16\\ 12x-9y=15\end{array}}$
⇔ ${\displaystyle \{\begin{array}{c}y=1\\ x=2\end{array}}$

Bài 2:

a) Đồ thị:

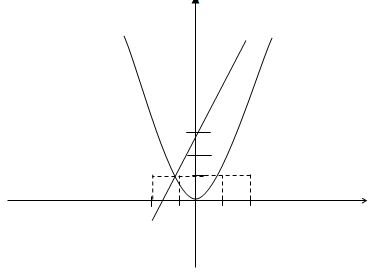
Lưu ý:  (P) đi qua O(0;0), ${\displaystyle (\pm 1;1),(\pm 2;4)}$

(D) đi qua (-1;1) , (3;9)

b) PT hoành độ giao điểm của (P) và (D) là

x² = 2x +3 ⇔ x² – 2x – 3 = 0 ⇔ x = -1 hay x = 3 (do a-b+c=0)

y(-1) = 1, y(3) = 9

Vậy toạ độ giao điểm của (P) và (D) là (-1;1) , (3;9)

Bài 3: Thu gọn các biểu thức sau

${\displaystyle A=\frac{5+\sqrt{5}}{\sqrt{5}+2}+\frac{\sqrt{5}}{\sqrt{5}-1}-\frac{3\sqrt{5}}{3+\sqrt{5}}}$

= ${\displaystyle \frac{(5+\sqrt{5})(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)}+\frac{\sqrt{5}(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)}-\frac{3\sqrt{5}(3-\sqrt{5})}{(3+\sqrt{5})(3-\sqrt{5})}}$

= ${\displaystyle 3\sqrt{5}-5+\frac{5+\sqrt{5}}{4}-\frac{9\sqrt{5}-15}{4}=3\sqrt{5}-5+\frac{5+\sqrt{5}-9\sqrt{5}+15}{4}}$

= ${\displaystyle 3\sqrt{5}-5+5-2\sqrt{5}=\sqrt{5}}$

Bài 4:
Cho phương trình ${\displaystyle x^2-mx-1=0}$ (1) (x là ẩn số)

a) Chứng minh phương trình (1) luôn có 2 nghiệm trái dấu
Ta có a.c = -1 < 0 , với mọi m nên phương trình (1) luôn có 2 nghiệm trái dấu với mọi m.

b) Gọi x1, x2 là các nghiệm của phương trình (1):

Tính giá trị của biểu thức:

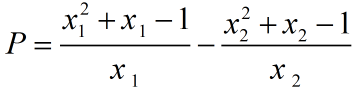
Ta có ${\displaystyle x_1^2=m{x}_1+1}$ và ${\displaystyle x_2^2=m{x}_2+1}$ (do x1, x2 thỏa 1)

Do đó:

Bài 5:

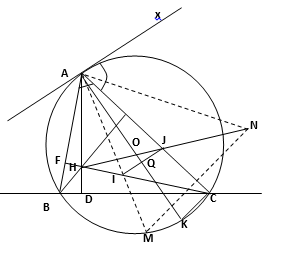
a) Ta có tứ giác BFHD nội tiếp do có 2 góc đối

F và D vuông ⇒ ${\displaystyle \widehat{FHD}=\widehat{AHC}={180}^0-\widehat{ABC}}$

b) ${\displaystyle \widehat{ABC}=\widehat{AMC}}$ cùng chắn cung AC

mà ${\displaystyle \widehat{ANC}=\widehat{AMC}}$ do M, N đối xứng

Vậy ta có ${\displaystyle \widehat{AHC}}$ và ${\displaystyle \widehat{ANC}}$ bù nhau

⇒ tứ giác AHCN nội tiếp

c) Ta sẽ chứng minh tứ giác AHIJ nội tiếp

Ta có ${\displaystyle \widehat{NAC}=\widehat{MAC}}$ do MN đối xứng qua AC mà ${\displaystyle \widehat{NAC}=\widehat{CHN}}$ (do AHCN nội tiếp)

⇒ ${\displaystyle \widehat{IAJ}=\widehat{IHJ}}$ ⇒ tứ giác HIJA nội tiếp.

⇒ ${\displaystyle \widehat{AJI}}$ bù với ${\displaystyle \widehat{AHI}}$ mà ${\displaystyle \widehat{ANC}}$ bù với ${\displaystyle \widehat{AHI}}$  (do AHCN nội tiếp)

⇒ ${\displaystyle \widehat{AJI}=\widehat{ANC}}$

Cách 2 :

Ta sẽ chứng minh IJCM nội tiếp

Ta có ${\displaystyle \widehat{AMJ}}$ = ${\displaystyle \widehat{ANJ}}$ do AN và AM đối xứng qua AC.

Mà ${\displaystyle \widehat{ACH}}$ = ${\displaystyle \widehat{ANH}}$ (AHCN nội tiếp) vậy ${\displaystyle \widehat{ICJ}}$ = ${\displaystyle \widehat{IMJ}}$

⇒ IJCM nội tiếp ⇒ ${\displaystyle \widehat{AJI}=\widehat{AMC}=\widehat{ANC}}$

d) Kẻ OA cắt đường tròn (O) tại K và IJ tại Q ta có ${\displaystyle \widehat{AJQ}}$ = ${\displaystyle \widehat{AKC}}$

vì ${\displaystyle \widehat{AKC}}$ = ${\displaystyle \widehat{AMC}}$ (cùng chắn cung AC), vậy ${\displaystyle \widehat{AKC}}$ = ${\displaystyle \widehat{AMC}}$ = ${\displaystyle \widehat{ANC}}$

Xét hai tam giác AQJ và AKC :

Tam giác AKC vuông tại C (vì chắn nửa vòng tròn ) 2 tam giác trên đồng dạng

Vậy ${\displaystyle \hat{Q}={90}^0}$ . Hay AO vuông góc với IJ

Cách 2 : Kẻ thêm tiếp tuyến Ax với vòng tròn (O) ta có ${\displaystyle \widehat{xAC}}$ = ${\displaystyle \widehat{AMC}}$

mà ${\displaystyle \widehat{AMC}}$ = ${\displaystyle \widehat{AJI}}$ do chứng minh trên vậy ta có ${\displaystyle \widehat{xAC}}$ = ${\displaystyle \widehat{AJQ}}$ ⇒ JQ song song Ax

Vậy IJ vuông góc AO (do Ax vuông góc với AO).