Căn bậc hai

Kiến thức cần nhớ

1. Căn bậc hai của số thực a là số x sao cho $x^{2}$ = a.

2. Cho số thực a không âm. Căn bậc hai số học của a (kí hiệu $sqrt{a}$ ) là một số x không âm mà bình phương của nó bằng a :

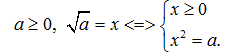
3. Với a, b là các số dương, ta có

a) Nếu a < b thì $sqrt{a}$ < $sqrt{b}$ ;

b) Nếu $sqrt{a}$ < $sqrt{b}$ thì a < b.

Ví dụ 1. So sánh :

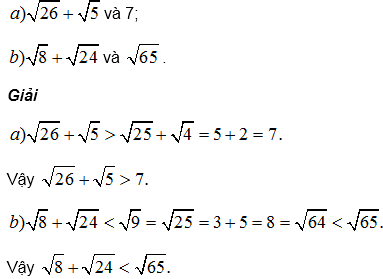
Ví dụ 2. Cho số a không âm.

a) Có thể khẳng định rằng $sqrt{a}$ ≤ a với mọi a hay không ?

b) Với các giá trị nào của a thì $sqrt{a}$ > a?

Giải

BÀI TẬP

1. Các biểu thức sau có thể nhận giá trị âm được không, có thể bằng 0 được không ?

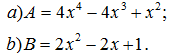
2. Tìm chỗ sai trong bài toán ngụỵ biện sau :

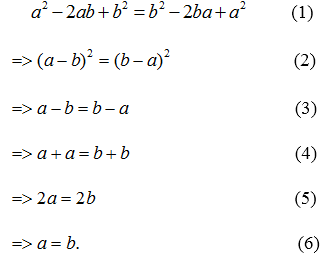
Vậy bất kì hai số nào cũng bằng nhau (!).

3. Cho x + y = 1. Tìm giá trị nhỏ nhất của biểu thức A = $x^{3}$ + $y^{3}$ .

4. Tìm giá trị của x sao cho :

a) |x – 3| = |x + 5| ; b) x(x – 3) ≥ 3(x – 3);

c) $x^{2}$ ≤ 4 ; d) $x^{2}$ ≥ 4.

5. Tìm liên hệ giữa các số a và b biết rằng |a + b| > |a – b|.

6. a) Chứng min h bất đẳng thức $(a + 1)^{2}$ ≥ 4a.

b) Cho các số dương a, b, c có tích bằng 1. Chứng minh rằng

(a + 1)(b + 1)(c + 1) ≥ 8.

7. Số nào lớn hơn :

8. Cho x ≥ 0. Tìm các giá trị của x sao cho :

a) $sqrt{x}$ ≥ x ; b) $sqrt{x}$ < x ; c) $sqrt{}$ ≤ x.

9. Cho hai số không âm a và b. Ta gọi trung bình nhân của hai số a và b là

$sqrt{ab}$ . Chứng minh rằng trung bình cộng của hai số a và b không nhỏ hơn trung bình nhân của chúng (bất đẳng thức Cô-si).

10. Cho các số a, b, c không âm. Chứng minh bất đẳng thức :

a + b + c ≥ $sqrt{ab}$ + $sqrt{bc}$ + $sqrt{ca}$ .

11. Tìm giá trị nhỏ nhất của biểu thức : A = $x^{4}$ – 6 $x^{2}$ + 10.

12. Cho biểu thức A = x – 2 $sqrt{x + 2}$ .

a) Đặt y = $sqrt{x + 2}$ . Hãy biểu thị A theo y.

b) Tìm giá trị nhỏ nhất của A.

Căn bậc hai – Bồi dưỡng Đại số 9