Đại số 8 – Chuyên đề 8 – Bất phương trình bậc nhất một ẩn

A. Lý thuyết

1. Bất đẳng thức

2. Liên hệ giữa thứ tự và phép cộng

Ví dụ: Cho $a>b\Rightarrow a+3>b+3$

3. Liên hệ giữa thứ tự và phép nhân

Ví dụ: $a>b\Rightarrow a.(-3)<b.\left(-3\right)$

4. Bất phương trình một ẩn

4.1 Nghiệm của bất phương trình

Ví dụ: x = 3 là nghiệm của bất phương trình $2x+3<10$.

$VT=2.3+3=9;VP=10$. Vì $9<10$ nên x = 3 là nghiệm của bất phương trình.

4.2 Tập nghiệm của bất phương trình

4.3 Biểu diễn tập nghiệm

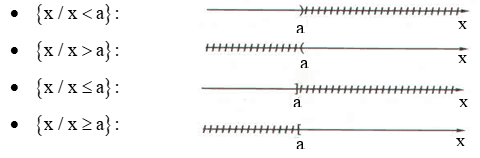
5. Bất phương trình bậc nhất một ẩn

5.1 Bất phương trình tương đương

Ví dụ: Hai bất phương trình $2x+1>0$ và $x>-\frac{1}{2}$ là hai bất phương trình tương đương.

5.2 Quy tắc chuyển vế

Ví dụ: $x+3<0\iff x<-3$

5.3 Quy tắc nhân

Ví dụ: $-x>-3\iff x<3$ (nhân cả hai vế với – 1 thì đổi chiều bất đẳng thức)

6. Phương trình chứa dấu giá trị tuyệt đối

Ví dụ: $\left|2x\right|=x-6$

– Với $x\ge 0$ ta có: $\left|2x\right|=x-6\iff 2x=x-6\iff x=-6$ (loại)

– Với $x<0$ ta có: $\left|2x\right|=x-6\iff -2x=x-6\iff x=2$ (loại)

B. Bài tập

Bài toán 1: Cho $a>b,$ so sánh:

a) $a-7$ và $b-7$           c) $a+30$ và $b+30$            e) $a-15$ và $b-15$

b) $6a$ và $6b$             d) $-5a$ và $-5b$                   f) $a+5$ và $b+3$

Bài toán 2: So sánh a và b nếu:

a) $a-7\le b-7$                  d) $35+a\ge 35+b$                  g) $a+13>b+13$

b) $-5a<-5b$                     e) $25+a\ge 25+b$                  h) $7a-8$ < $7b-8$

c) $a-10\le b-10$               f) $-14a+7$ >$-14b+7$   i) $2a<2b+1$

Bài toán 3: Cho $a>0,b>0$ và $a>b$. Chứng tỏ rằng $\frac{1}{a}<\frac{1}{b}$.

Bài toán 4: Cho a, b là hai số bất kì, chứng tỏ rằng $\frac{a^2+b^2}{2}\ge ab$.

Bài toán 5: Cho a, b là hai số dương, chứng tỏ rằng $\frac{a}{b}+\frac{b}{a}\ge 2$.

Bài toán 6: Chứng minh bất đẳng thức:

a) $a^2+b^2+1\ge ab+a+b$                           d) $x^2+y^2+z^2+3\ge 2\left(x+y+z\right)$

b) $a^2+b^2+c^2\ge a\left(b+c\right)$ e) $\frac{x^2+y^2+z^2}{3}\ge {\left(\frac{x+y+z}{3}\right)}^2$

c) ${\left(x+y\right)}^2\le 2\left(x^2+y^2\right)$

Bài toán 7: Chứng minh bất đẳng thức

a) $\frac{1}{1.3}+\frac{1}{3.5}+\dots +\frac{1}{\left(2n-1\right)\left(2n+1\right)}<\frac{1}{2}$

b) $\frac{1}{1^2}+\frac{1}{2^2}+\dots +\frac{1}{n^2}<\frac{5}{3}$ với $n>1$

c) $\frac{1}{15}<\frac{1}{2}.\frac{3}{4}\dots \frac{99}{100}<\frac{1}{10}$

Bài toán 8: Thử xem $x=-1$ có là nghiệm của bất phương trình sau không?

a) $3x-7>2x+1$                         c) $7-3x<2-5x$

b) $-3x-1>x+1$                          d) $5\left(x-2\right)>3x-1$

Bài toán 9: Kiểm tra xem $x=-2$ có là nghiệm của bất phương trình sau không?

a) $3x+5>-9$                                     c) $10-4x>7x-12$

b) $-5x<2x+3$                                   d) $-8x-7<-6x-8$

Bài toán 10: Viết tập nghiệm của bất phương trình sau bằng kí hiệu tập hợp và biểu diễn tập nghiệm đó trên trục số:

a) $x>4$                       c) $x\ge -1$               e) $x>7$                    g) $x\ge -2$

b) $x<-2$                      d) $x\le 3$                  f) $x<0$                     h) $x\le -3$

Bài toán 11: Cho tập hợp $A=\left\{x\in \mathbb{N}/-10\le x\le 10\right\}.$ Tìm $x\in A$ là nghiệm của bất phương trình:

a) $\left|x\right|<4$                      b) $\left|x\right|>7$

c) $\left|x\right|\le 2$                    d) $\left|x\right|\ge 9$

Bài toán 12: Viết bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau:

a) Tổng của một số nào đó và 11 lớn hơn 17;

b) Hiệu của 15 và một số nào đó nhỏ hơn – 13;

c) Tổng của 3 lần số đó và 7 lớn hơn 8;

d) Hiệu của 10 và 5 lần số đó nhỏ hơn 15;

e) Tổng hai lần số đó và số 3 thì lớn hơn 18;

f) Hiệu của 5 và 3 lần số nào đó nhỏ hơn hoặc bằng 10.

Bài toán 13: Chứng minh các bất phương trình sau:

a) $x^2+x+1>0$ có nghiệm                       c) $\left(x-1\right)\left(x-5\right)+10<0$ vô nghiệm

b) $-x^2+3x-3<0$ có nghiệm                     d) $x^2+2x<2x$ vô nghiệm

Bài toán 14: Giải các bất phương trình sau:

Bài toán 15: Giải các bất phương trình sau (a là số cho trước):

a) $2x-3a\ge 0$

b) $a+1-5x\ge 0$

c) $\left(a-1\right)x+2a+1>0$ với $a>1$

d) $\left(2a+1\right)x-1-a\ge 0$ với $a<-\frac{1}{2}$

e) $\left(a^2+1\right)x+a-1<0$

f) $\left(a^2-2a+2\right)x\ge 2a+3$

Bài toán 16: Viết thành bất phương trình và giải:

a) Tìm x sao cho biểu thức $x-3,5$ nhận giá trị âm;

b) Tìm x sao cho biểu thức $x+11$ nhận giá trị dương;

c) Tìm x sao cho biểu thức $3x-5$ lớn hơn 4;

d) Tìm x sao cho giá trị của biểu thức $5x-4$ lớn hơn giá trị của biểu thức $3x-12.$

Bài toán 17: Tìm các giá trị của x thỏa mãn cả hai bất phương trình:

$\frac{{\left(x-3\right)}^2}{3}-\frac{{\left(2x-1\right)}^2}{12}\le x$             (1)

$2+\frac{3\left(x+1\right)}{3}<3-\frac{x-1}{4}$           (2)

Bài toán 18: Tìm các số nguyên x thỏa mãn cả hai bất phương trình:

$\frac{x-5}{4}-\frac{2x-1}{2}\le 3$                          (1)

$\frac{2x-3}{3}<\frac{x+1}{2}$                     (2)

Bài toán 19: Tìm giá trị của m để mỗi bất phương trình sau có nghiệm dương:

a) $\frac{x+1}{1-m}+\frac{x-1}{1+m}=\frac{x+m}{1+m}+\frac{2\left(x-m\right)}{1-m}$

b) $4-m=\frac{2}{x+1}$

Bài toán 20: Tìm giá trị của m để mỗi bất phương trình sau có nghiệm âm

a) $0,5\left(5x-1\right)=4,5-2m\left(x-2\right)$

b) $\frac{3mx+12m+5}{9m^2-1}=\frac{2x-3}{3m+1}-\frac{3x-4m}{1-3m}$

Bài toán 21: Tìm các giá trị nguyên của x để biểu thức $A=\frac{x-1}{5}-\frac{x-2}{3}$ có giá trị lớn hơn 1 nhứng nhỏ hơn 3.

Bài toán 22: Với giá trị nào của a thì phương trình $\frac{a+1}{x-1}=1-a$ có nghiệm dương nhỏ hơn 1.

Bài toán 23: Xác định m để bất phương trình $\left(m^2-4m+3\right)x+m-m^2<0$ nghiệm đúng với mọi x.

Bài toán 24: Giải phương trình

Bài toán 25: Giải phương trình

a) $\frac{\left|x\right|-1}{4}-\frac{1}{8}\left(\frac{\left|x\right|-5}{4}-\frac{14-2\left|x\right|}{5}\right)=\frac{\left|x\right|-9}{2}-\frac{7}{8}$

b) $\frac{7x+5}{5}-x=\frac{\left|3x-5\right|}{2}$

c) $x-\frac{\left|3x-2\right|}{5}=3-\frac{2x-5}{3}$

Bài toán 26: Giải phương trình

a) $x^2-\left|x\right|=6$                                      e) $\left|x+1\right|-\left|2-x\right|=0$

b) $\left|x^2-4\right|=x^2-4$                      f) $\left|x\right|-\left|x-2\right|=2$

c) $\left|2x-x^2-1\right|=2x-x^2-1$            g) $\left|x-1\right|+\left|x-2\right|=1$

d) $\left|x^2-3x+3\right|=3x-x^2-1$           h) $\left|x-2\right|+\left|x-3\right|+\left|2x-8\right|=9$

Bài toán 27: Giải phương trình

a) $3x\left|x+1\right|-2x\left|x+2\right|=12$

b) $\frac{x^2-4-\left|x-2\right|}{2}=x\left(x+1\right)$

c) $\frac{x^3+x^2-x}{x\left|x-2\right|}=1$

d) $\frac{7}{8x}+\frac{5-x}{4x^2-8x}=\frac{x-1}{2x\left(x-2\right)}+\frac{1}{8x-16}$

e) $\frac{x+2}{x^2+2x+4}-\frac{x-2}{x^2-2x+4}=\frac{6}{x\left(x^4+4x^2+16\right)}$

f) $\frac{x^2-x}{x+3}-\frac{x^2}{x-3}=\frac{7x^2-3x}{9-x^2}$

Bài toán 28: Giải bất phương trình

a) $\left|2x+5\right|\le \left|7-4x\right|$

b) $\left|\frac{2-3\left|x\right|}{1+x}\right|\le 1$

c) $\frac{\left|x^2-4x\right|+3}{x^2+\left|x-5\right|}\ge 1$

d) $\frac{9}{\left|x-5\right|-3}\ge \left|x-3\right|$

e) $\left|2x-1\right|\ge x-1$

f) $\left|2x+5\right|>\left|7-4x\right|$

Bài toán 29: Giải và biện luận bất phương trình

a) $-1\le \frac{x+m}{mx+1}\le 1$
b) $\frac{x-m}{x+1}=\frac{x-2}{x-1}$
c) $\frac{ax-1}{x–1}+\frac{b}{x+1}=\frac{a\left(x^2+1\right)}{x^2-1}$

Bài toán 30: Chứng minh các bất đẳng thức

a) $a^2+b^2\ge \frac{1}{2}$ với $a+b=1;$

b) $a^2+b^2+c^2\ge \frac{1}{3}$ với $a+b+c=1$

c) ${a_1}^2+{a_2}^2+\dots +{a_n}^2\ge \frac{1}{n}$ với $a_1+a_2+\dots +a_n=1$

Bài toán 31: Cho biểu thức

$M=\left[\frac{3\left(x+2\right)}{2\left(x^3+x^2+x+1\right)}+\frac{2x^2-x-10}{2\left(x^3+x^2+x+1\right)}\right]:\left[\frac{5}{x^2+1}+\frac{3}{2\left(x+1\right)}-\frac{3}{2\left(x-1\right)}\right].\frac{2}{x-1}$

a) Rút gọn M;

b) Tính giá trị của M biết $\left|x\right|=\frac{1}{3};$

c) Tìm x biết $\left|M\right|=2004;$

d) Tìm giá trị của x để $M>0,$ $M<0;$

e) Tìm các giá trị nguyên của x để giá trị của biểu thức M là số nguyên.

Bài toán 32: Trong một buổi lao động trồng cây, cô giáo chủ nhiệm đã phân công cho các tổ lần lượt như sau:

Tổ I trồng 20 cây và 4% số cây còn lại.

Tổ II trồng 21 cây và 4% số cây còn lại.

Tổ II trồng 22 cây và 4% số cây còn lại.

Cứ chia như vậy cho đến tổ cuối cùng thì vừa hết số cây và số cây mỗi tổ trồng đều bằng nhau. Hỏi lớp đó có bao nhiêu tổ, số cây lớp trồng được là bao nhiêu?

Bài toán 33: Trong một lớp có 14 học sinh giỏi Toán, 13 học sinh giỏi Văn. Số học sinh vừa giỏi Toán, vừa giỏi Văn bằng một nửa số học sinh không giỏi Toán mà cũng không giỏi Văn. Hỏi có bao nhiêu học sinh vừa giỏi Toán, vừa giỏi Văn, biết rằng số học sinh của lớp đó là 35.