Đề kiểm tra khảo sát chất lượng môn Toán lớp 7, Phòng giáo dục và đào tạo quận Hà Đông, TP Hà Nội năm học 2018-2019.
Thời gian làm bài: 60 phút
Đề thi gồm 2 phần Trắc nghiệm và Tự luận.
I. TRẮC NGHIỆM KHÁCH QUAN (1 điểm)
Chọn chữ cái đứng trước câu trả lời đúng (viết vào bài làm).
Câu 1. Nếu $ \sqrt{{x+1}}=3$ thì $ {{x}^{2}}$ có giá trị là
A. 8
B. 2
C. 64
D. $ \pm 64$
Câu 2. Cho $ 12:a=6:b$. Tỉ lệ thức nào dưới đây là sai?
A. $ \frac{a}{6}=\frac{b}{{12}}$
B. $ \frac{a}{{12}}=\frac{b}{6}$
C. $ \frac{{12}}{a}=\frac{6}{b}$
D. $ \frac{a}{b}=\frac{{12}}{6}$
Câu 3. Phân số nào sau đây viết được dưới dạng số thập phân hữu hạn?
A. $ \frac{5}{{14}}$
B. $ \frac{7}{9}$
C. $ \frac{{-8}}{{15}}$
D. $ \frac{9}{{24}}$
Câu 4. Cho hình vẽ và biết $ a//b$, thì:
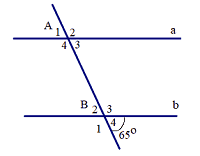
A. $ \widehat{{{{A}_{1}}}}={{115}^{o}}$
B. $ \widehat{{{{A}_{4}}}}={{115}^{o}}$
C. $ \widehat{{{{A}_{3}}}}={{115}^{o}}$
D. $ \widehat{{{{A}_{2}}}}={{65}^{o}}$
II. TỰ LUẬN (9 điểm)
Bài 1. (2 điểm) Tính giá trị của các biểu thức:
a) $ A=3\frac{1}{7}-\left( {5.0,05+\frac{{22}}{7}} \right)-(4+0,75)$
b) $ B=\frac{{{{{(-1)}}^{{2018}}}.{{{\left( {\frac{2}{5}} \right)}}^{3}}.{{{\left( {\frac{{15}}{4}} \right)}}^{2}}}}{{\frac{{{{{15}}^{2}}}}{{{{2}^{4}}}}.{{{\left( {\frac{2}{5}} \right)}}^{3}}}}$
Bài 2. (3,5 điểm) Tìm $ x,y$ biết:
a) $ {{2}^{3}}{{.2}^{x}}-2,1=13,9$
b) $ \left| {x-\frac{3}{2}} \right|=\sqrt{{0,25}}$
c) $ \frac{x}{2}=\frac{y}{7}$ và $ 2x-5y=93$
Bài 3. (2,5 điểm) Cho hình vẽ, biết Ax//By,
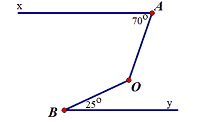
$ \widehat{{xAO}}={{70}^{o}},\widehat{{OBy}}={{25}^{o}}$
a) Tính góc $ \widehat{{AOB}}$
b) Qua B vẽ đường thẳng d song song với AO cắt tia Ax tại M. Tính $ \widehat{{MBO}}$
Bài 4. (1 điểm) Cho 4 số $ {{a}_{1}},{{a}_{2}},{{a}_{3}},{{a}_{4}}$ khác 0 và thỏa mãn: $ a_{2}^{2}={{a}_{1}}.{{a}_{3}}$ và $ a_{3}^{2}={{a}_{2}}.{{a}_{4}}$
Chứng minh rằng: $ \frac{{a_{1}^{3}+a_{2}^{3}+a_{3}^{3}}}{{a_{2}^{3}+a_{3}^{3}+a_{4}^{3}}}=\frac{{{{a}_{1}}}}{{{{a}_{4}}}}$