1. Khái niệm hình chóp
– Hình chóp có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này gọi là đỉnh của hình chóp.
– Đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao của hình chóp.
– Hình chóp có đáy là tam giác gọi là hình chóp tam giác
– Hình chóp có đáy là tứ giác gọi là hình chóp tứ giác.
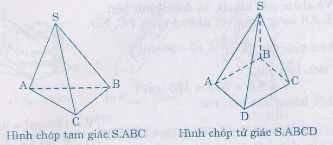
Hình chóp tam giác và hình chóp tứ giác
2. Hình chóp đều
– Hình chóp đều là hình chóp có mặt đáy là một đa giác đều, có mặt bên là những tam giác cân bằng nhau có chung đỉnh.
Trên hình chóp đều S.ABCD:
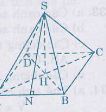
– Chân đường cao H là tâm của đường tròn đi qua các đỉnh của mặt đáy
– Đường cao vẽ từ đỉnh S của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
a. Công thức tính diện tích xung quanh hình chóp đều
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn.
Sxq = pd
p: nửa chu vi đáy
d: trung đoạn của hình chóp đều
b. Công thức tính thể tích hình chóp đều
Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao
$ \displaystyle V=\frac{1}{3}S.h$
S: diện tích đáy
h: chiều cao
3. Hình chóp cụt đều
Cắt hình chóp đều bằng một mặt phẳng song song với đáy. Phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy của hình chóp là một hình chóp cụt đều.
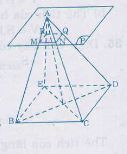
Hình chóp cụt đều
Nhận xét: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.