Đề thi tuyển sinh môn Toán vào lớp 10 trung học phổ thông năm học 2017 – 2018. Sở giáo dục và đào tạo Bình Dương. Có đáp án.
Thời gian làm bài 120 phút (không kể phát đề).
Đề thi:
Bài 1 : (1 điểm) Rút gọn biểu thức sau:
1) $ A=3\sqrt{3}+2\sqrt{12}-\sqrt{27}$; 2) $ B=\sqrt{{{\left( 3-\sqrt{5} \right)}^{2}}}+\sqrt{6-2\sqrt{5}}$.
Bài 2: (1.5 điểm) Cho parabol (P): $ y={{x}^{2}}$ và đường thẳng (d): $ y=4x+9$.
1) Vẽ đồ thị (P);
2) Viết phương trình đường thẳng $ ({{d}_{1}})$ biết $ ({{d}_{1}})$ song song (d) và $ ({{d}_{1}})$ tiếp xúc (P).
Bài 3 :(2,5 điểm)
1) Giải hệ phương trình $ \left\{ \begin{array}{l}2x-y=5\\x+5y=-3\end{array} \right.$ . Tính $ P={{\left( x+y \right)}^{2017}}$ với x, y vừa tìm được.
2) Cho phương trình $ {{x}^{2}}-10mx+9m=0\,\,(1)$ (m là tham số)
a) Giải phương trình (1) với m = 1;
b) Tìm các giá trị của tham số m để phương trình (1) có hai nghiệm $ {{x}_{1}},\,{{x}_{2}}$ phân biệt thỏa điều kiện $ {{x}_{1}}-9{{x}_{2}}=0$.
Bài 4:(1,5 điểm) Hai đội công nhân đắp đê ngăn triều cường. Nếu hai đội cùng làm thì trong 6 ngày xong việc. Nếu làm riêng thì đội I hoàn thành công việc chậm hơn đội II là 9 ngày. Hỏi nếu làm riêng thì mỗi đội đắp xong đê trong bao nhiêu ngày?
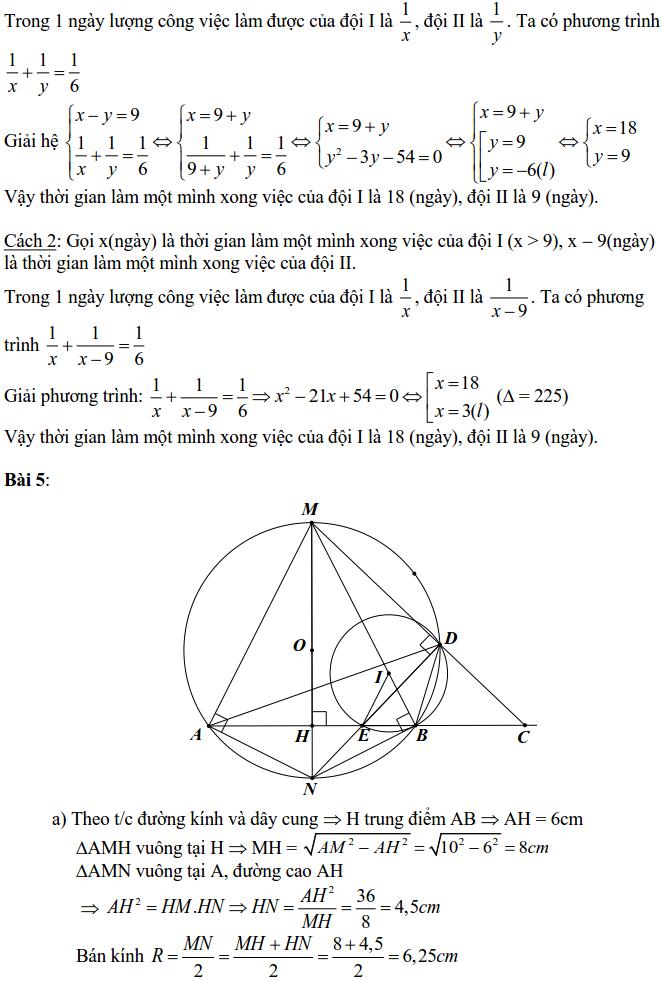
Bài 5: (3,5 điểm) Tam giác AMB cân tại M nội tiếp trong đường tròn (O; R). Kẻ MH vuông góc AB (HÎAB), MH cắt đường tròn tại N. Biết MA = 10cm, AB = 12cm.
a) Tính MH và bán kính R của đường tròn;
b) Trên tia đối tia BA lấy điểm C. MC cắt đường tròn tại D, ND cắt AB tại E. Chứng minh tứ giác MDEH nội tiếp và chứng minh các hệ thức sau: $ N{{B}^{2}}=NE.ND$ và $ AC.BE=BC.AE$;
c) Chứng minh NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE.
Đáp án: