Đề thi tuyển sinh vào lớp 10 môn Toán trường THPT chuyên thành phố Hải Phòng năm học 2013 – 2014.
Bài 1. (2.0 điểm)
a) Cho $ A=\left( \frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{x\sqrt{x}-8} \right):\frac{\sqrt{x}+7}{x+2\sqrt{x}+4}$. Tìm sao cho A < 2.
b) Tìm m để phương trình $ {{x}^{2}}-\left( 2m+4 \right)x+3m+2=0$ có hai nghiệm phân biệt $ {{x}_{1}},{{x}_{2}}$ thỏa mãn $ {{x}_{2}}=2{{x}_{1}}+3$.
Bài 2. (2.0 điểm)
a) Giải phương trình $ \sqrt{5x-1}-\sqrt{3x+13}=\frac{x-7}{3}$.
b) Giải hệ phương trình $ \left\{ \begin{array}{l}2{{x}^{2}}+xy={{y}^{2}}-3y+2\\{{x}^{2}}-{{y}^{2}}=3\end{array} \right.$.
Bài 3. (3.0 điểm)
Cho hai điểm A, B cố định. Một điểm C khác B di chuyển trên đường tròn (O) đường kính AB sao cho AC > BC. Tiếp tuyến của đường tròn (O) tại C cắt tiếp tuyến tại A ở D, cắt AB ở E. Hạ AH vuông góc với CD tại H.
a) Chứng minh rằng AD.CE = CH.DE.
b) Chứng minh rằng OD.BC là một hằng số.
c) Giả sử đường thẳng đi qua E, vuông góc với AB cắt AC, BD lần lượt tại F, G. Gọi I là trung điểm AE. Chứng minh rằng trực tâm tam giác IFG là một điểm cố định.
Bài 4. (1.0 điểm)
a) Chứng minh rằng nếu $ x\ge y\ge 1$ thì $ x+\frac{1}{x}\ge y+\frac{1}{y}$.
b) Cho $ 1\le a,b,c\le 2$. Chứng minh rằng $ \left( a+b+c \right)\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\le 10$.
Bài 5. (2.0 điểm)
a) Cho a, b là hai số nguyên dương thỏa mãn và cùng chia hết cho 21. Tìm số dư của phép chia $ A={{4}^{a}}+{{9}^{b}}+a+b$ cho 21.
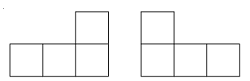
b) Có thể phủ kín bảng 20 x 13 ô vuông bằng các miếng lát có một trong hai dạng dưới (có thể xoay và sử dụng đồng thời cả hai dạng miếng lát) sao cho các miếng lát không chờm lên nhau không?
