1. Khái niệm hình nón
Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
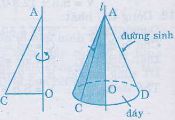
– Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
– Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
– A là đỉnh và AO là đường cao của hình nón.
2. Diện tích xung quanh, diện tích toàn phần của hình nón
Diện tích xung quanh của hình nón:
Diện tích toàn phần của hình nón:
(r là bán kính đường tròn đáy, l là đường sinh)
3. Thể tích hình nón
Công thức tính thể tích hình nón: Vnón =
Diện tích toàn phần của hình nón:
(r là bán kính đường tròn đáy, l là đường sinh)
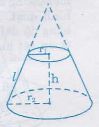
4. Thể tích hình nón cụt
Công thức tính thể tích hình nón: Vnón =