Phương trình bậc nhất hai ẩn
Kiến thức cần nhớ
Phương trình bậc nhất hai ẩn là phương trình có dạng ax + by = c, trong đó x và y là các ẩn ; a, b, c là các số đã biết, a và b không đồng thời bằng 0.
Đồ thị của phương trình ax + by = c là một đường thẳng.
Ví dụ 15.
Cho phương trình
ax + by = c (a và b không đồng thời bằng 0). (1)
Đường thẳng biểu diễn phương trình có dạng như thế nào nếu :
a) a ≠ 0, b ≠ 0 ;
b) a = 0, b ≠ 0 ;
c) a ≠ 0, b = 0.
Giải
a) Nếu a 0, b ≠ 0 thì phương trình (1) trở thành y = x
.
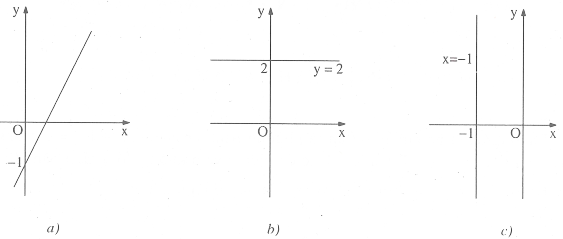
Khi đó đồ thị cắt cả hai trục toạ độ (chẳng hạn đường thẳng 2x – y = 1 ở hình 2a ; y = 2x – 1 là hàm số bậc nhất).
b) Nếu a = 0, b ≠ 0 thì (1) có dạng y = .
Khi đó đường thẳng (1) vuông góc với trục tung (chẳng hạn đường thẳng y = 2 ở hình 2b ; y = 2 là hàm hằng số). Đặc biệt, nếu c = 0 ta có phương trình của trục hoành y = 0.
c) Nếu a ≠ 0, b = 0 thì (1) có dạng x = .
Khi đó đường thẳng sẽ vuông góc với trục hoành (chẳng hạn đường thẳng x = -1 ở hình 2c ; chú ý rằng x= -1 không phải là hàm số vì ứng với một giá trị của x có nhiều hơn một giá trị tương ứng của y). Đặc biệt nếu c = 0 ta có phương trình của trục tung x = 0.
Ví dụ 16.
Tìm các số nguyên x, y thoả mãn mỗi phương trình sau :
![]()
Giải
![]()
Đặt x 1 = 2k (k ∈ Z) thì x = 2k – 1, y = 3(2k -1) k = 7k – 3. Các số nguyên x, y thoả mãn phương trình đã cho là x = 2k – 1, y = 7k – 3 với k ∈ Z .
b) Biểu thị y theo x được
![]()
Đặt x – 1 = 3k (k ∈ Z) thì x = 3k 1, y = 3(3k 1) – 1 k = 10k 2.
Các số nguyên x, y thoả mãn phương trình đã cho là x = 3k 1, y = 10k 2 với k ∈ Z.
BÀI TẬP
71. Chứng minh rằng khi a thay đổi, các đường thẳng ax 5y = 2 luôn đi qua một điểm cố định.
72. Xét các đường thẳng d có phương trình
(m 2)x (m – 3)y – m 8 = 0.
73. Chứng minh rằng với mọi m, các đường thẳng luôn luôn đi qua điểm A(-1; 2).
73*. Chứng minh rằng khi m thay đổi, các đường thẳng 2x (m – 1)y = 1 luôn luôn đi qua một điểm cố định.
74. Vẽ đồ thị của các hàm số :
a) y = ; ‘ b) y = 2x |1 – 2x|.
75. Cho hàm số
y = |x| |1 – x|.
a) Vẽ đồ thị của hàm số.
b) Dùng đồ thị để tìm giá trị nhỏ nhất của biểu thức |x| |1 – x|.
c) Dùng đồ thị để tìm số nghiệm của phương trình |x| |1 – x| nếu m = 1, m > 1, m < 1.
76. Tìm nghiệm nguyên của các phương trình :
a) 6x y = 5 ; b) 4x 3y = 20 ; c) 12x – 5y = 2.
77. Tìm nghiệm nguyên dương của các phương trình :
a) 4x 11y = 47 ; b) 1 lx 18y = 120.
78. Tìm nghiệm nguyên dương của các phương trình :
a) xy – 2x 3y = 27 ; b) x(y 3) – y = 38 ;
b) 3xy x y = 17 ; d) x 1 = xy – y.
79. a) Vẽ đồ thị của phương trình 2x – 3y = 6.
b) Biết rằng đường thẳng 2x – 3y = 6 chia mặt phẳng toạ độ thành hai miền (không kể đường thẳng 2x – 3y = 6) : một miền gồm các điểm cố toạ độ (x ; y) mà hoành độ và tung độ thoả mãn bất phương trình 2x – 3y < 6, miền còn lại gồm các điểm có toạ độ (x ; y) mà hoành độ và tung độ thoả mãn bất phương trình 2x – 3y > 6. Hãy xác định hai miền đó trên hình vẽ.