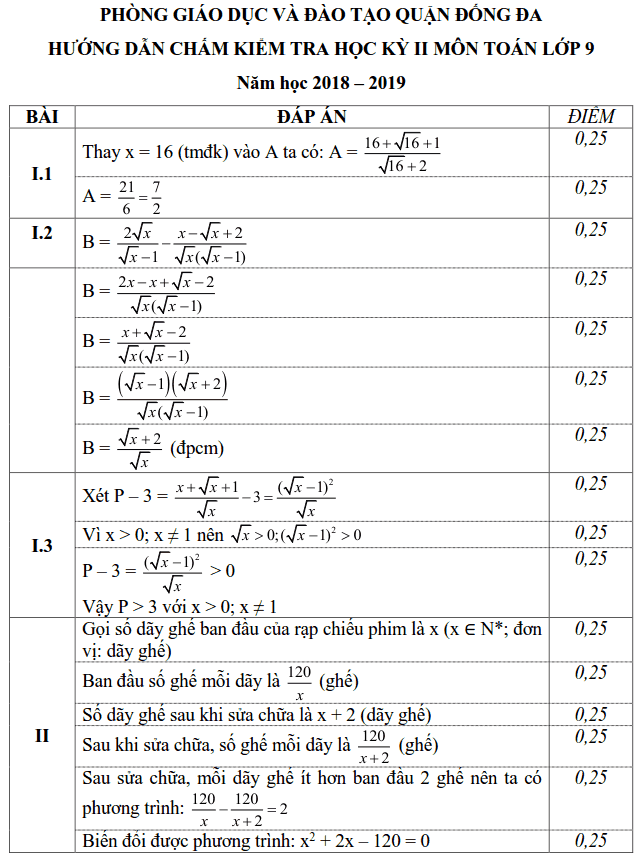Đề thi học kì 2 môn Toán lớp 9 quận Đống Đa, Hà Nội năm học 2018-2019. Ngày kiểm tra: 10 tháng 04 năm 2019. Thời gian làm bài: 90 phút.
Bài I. (2,5 điểm)
Cho biểu thức A = $ \frac{{x+\sqrt{x}+1}}{{\sqrt{x}+2}}$ và B = $ \frac{{2\sqrt{x}}}{{\sqrt{x}-1}}-\frac{{x-\sqrt{x}+2}}{{x-\sqrt{x}}}$ với x > 0; x ≠ 1
1) Tính giá trị của A khi x = 16
2) Chứng minh rằng B = $ \frac{{\sqrt{x}+2}}{{\sqrt{x}}}$
3) Cho P = A.B. So sánh P với 3.
Bài II. (2,0 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một rạp chiếu phim có 120 chỗ ngồi được sắp xếp thành những dãy ghế, mỗi dãy ghế có số ghế như nhau. Sau đó, khi sửa chữa người ra đã bổ sung thêm hai dãy ghế. Để giữ nguyên số ghế của rạp, mỗi dãy ghế được kê ít hơn so với ban đầu là 2 ghế. Hỏi trước khi sửa chữa thì rạp chiếu phim có bao nhiêu dãy ghế?
Bài III. (1,5 điểm) Cho phương trình: x2 – (m + 4)x + 4m = 0 (m là tham số)
1) Giải phương trình khi m = – 1
2) Tìm m để phương trình đã cho có 2 nghiệm phân biệt x1; x2 thỏa mãn x12 + (m + 4)x2 = 16.
Bài IV. (3,5 điểm) Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC < BC; E là một điểm thuộc đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH vuông góc với AB tại H.
1) Chứng minh tứ giác ACEH là tứ giác nội tiếp.
2) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.
3) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.
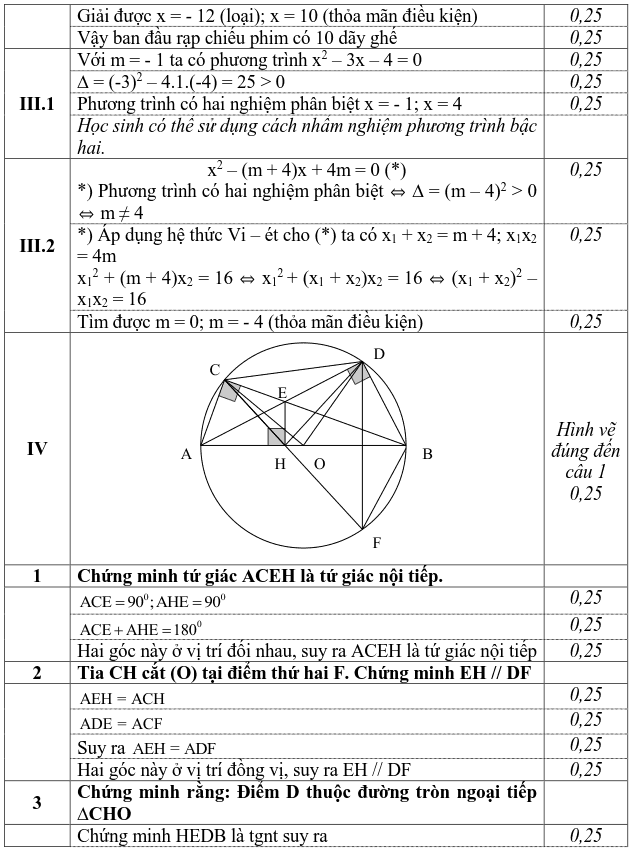
4) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng minh rằng AB, DF, IK cùng đi qua một điểm.
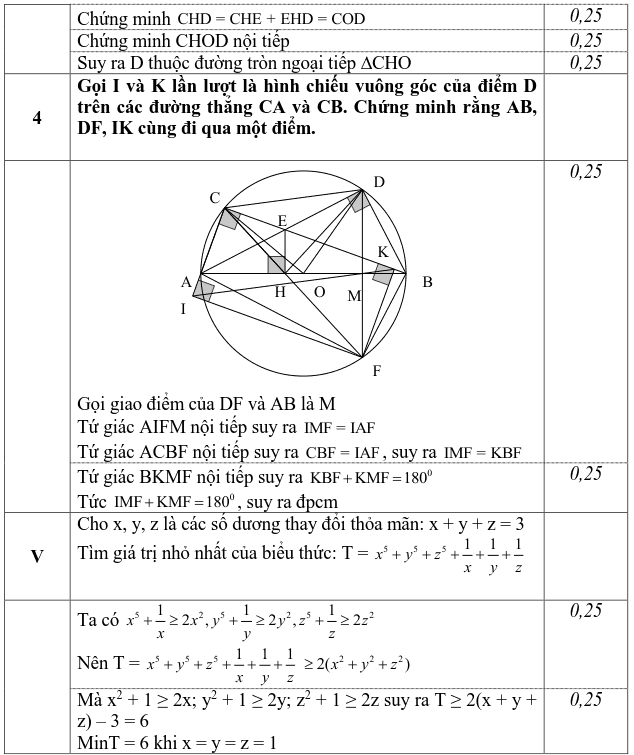
Bài V. (0,5 điểm). Cho x, y, z là các số dương thay đổi thỏa mãn: x + y + z = 3
Tìm giá trị nhỏ nhất của biểu thức: T = $ {{x}^{5}}+{{y}^{5}}+{{z}^{5}}+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$
Hướng dẫn giải đề kiểm tra HK2 môn Toán 9 quận Đống Đa 2018-2019: