Đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Thuận năm học 2018-2019
Thời gian làm bài: 120 phút (không kể thời gian giao đề). Ngày thi 11/07/2018.
Câu 1. Rút gọn biểu thức: $ \displaystyle A=(\sqrt{6}+\sqrt{2})\cdot \sqrt{2}+\sqrt{{16}}-\sqrt{{12}}$
Câu 2. Giải phương trình và hệ phương trình sau:
a) $ \displaystyle {{x}^{2}}-3x-10=0$
b) $ \displaystyle \left\{ {\begin{array}{*{20}{l}} {2x+y=4} \\ {3x-y=1} \end{array}} \right.$
Câu 3. Cho hàm số y = x2 có đồ thị (P)
a) Vẽ đồ thị hàm số (P) trên mặt phẳng tọa độ (Oxy)
b) Tìm tham số m để phương trình đường thẳng (d): $ \displaystyle y=\left( {{{m}^{2}}-4} \right)x+{{m}^{2}}-3$ luôn cắt P tại hai điểm phân biệt
Câu 4. Quãng đường AB dài 120 km. Hai ô tô khởi hành cùng một lúc từ A đến B. Mỗi giờ ô tô thứ nhất chạy nhanh hơn ô tô thứ hai 12 km nên đến trước ô tô thứ hai 30 phút. Tính vận tốc của ô tô thứ nhất.
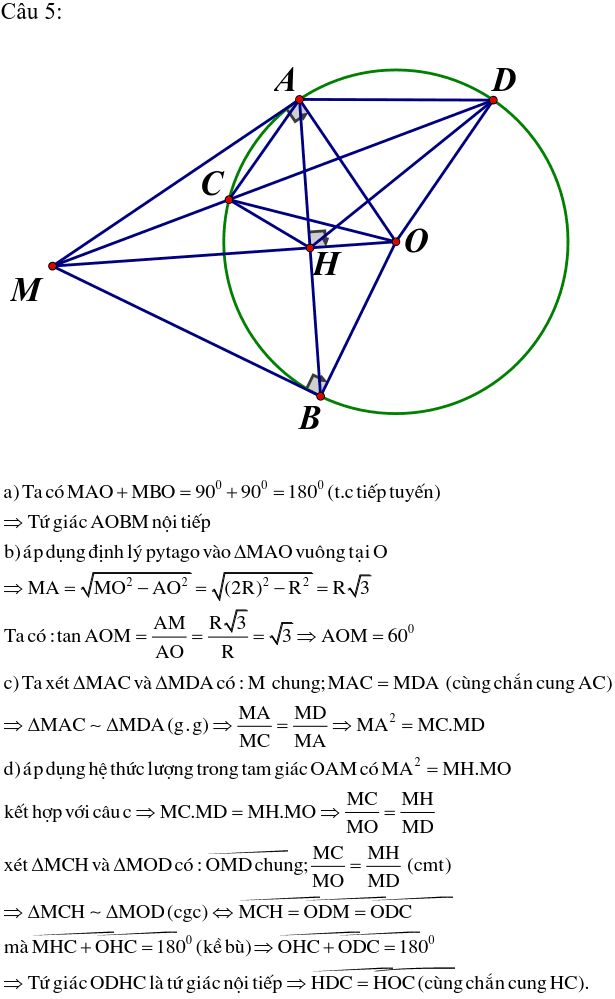
Câu 5. Cho đường tròn (O;R) và điểm M nằm ở ngoài đường tròn (O) sao cho OM=2R. Từ điểm M ve hai tiếp tuyến MA, MB với đường tròn (O) (A,B là các tiếp điểm)
a) Chứng minh tứ giác AOBM nội tiếp
b) Tính độ dài đoạn thẳng MA theo R và tính số đo $ \displaystyle \widehat{{AOM}}$
c) Từ M vẽ cát tuyến MCD đến đường tròn (O) (cát tuyến MCD không đi qua tâm và MC< MD). Chứng minh MA2 = MC.MD
d) AB cắt MO tại H. Chứng minh $ \displaystyle \widehat{{HDC}}=\widehat{{HOC}}$.
Đáp án đề thi vào 10 môn Toán tỉnh Bình Thuận 2018-2019:
