Câu 1: (1,0 điểm) Rút gọn biểu thức T = $ \sqrt{36}+\sqrt{9}-\sqrt{49}$
Câu 2: (1,0 điểm) Giải phương trình x2 – 5x – 14 = 0
Câu 3: (1,0 điểm) Tìm m để đường thẳng $ (d):y=\left( 2m-1 \right)x+3$ song song với đường thẳng $ (d’):y=5x+6$
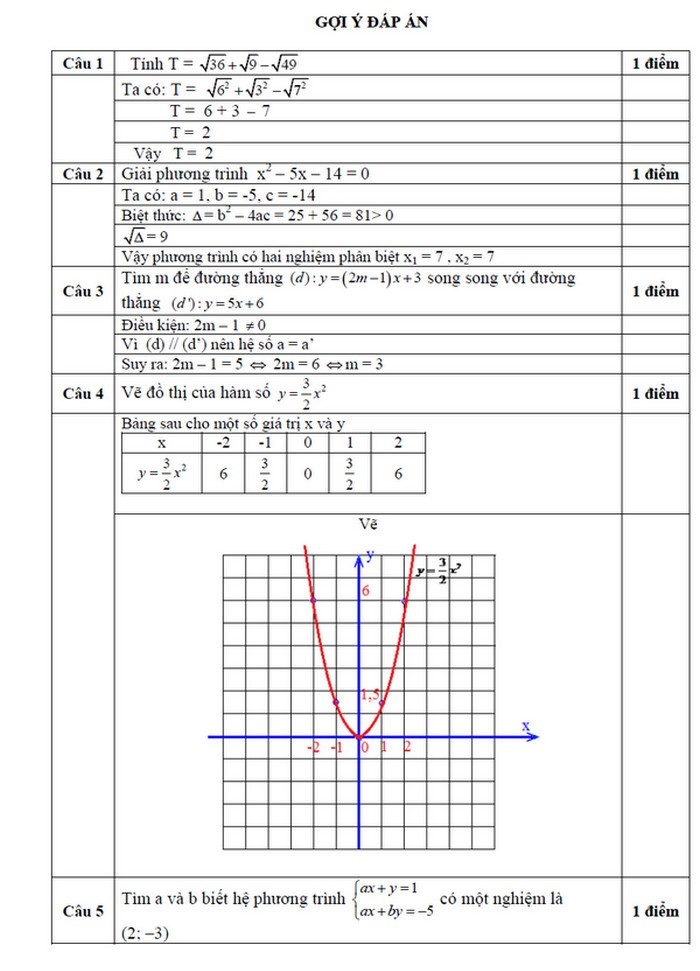
Câu 4: (1,0 điểm) Vẽ đồ thị của hàm số $ y=\frac{3}{2}{{x}^{2}}$
Câu 5: (1,0 điểm) Tìm a và b biết hệ phương trình $ \left\{ \begin{array}{l}ax+y=1\\ax+by=-5\end{array} \right.$ có một nghiệm là (2;–3)
Câu 6: Cho tam giác ABC vuông tại A có đường cao AH (H thuộc cạnh BC) biết AB = a , BC = 2a. Tính theo a độ dài AC và AH.
Câu 7: (1,0 điểm) Tìm m để phương trình $ {{x}^{2}}+x-m+2=0$ có hai nghiệm phân biệt x1, x2 thỏa $ {{x}_{1}}^{3}+{{x}_{2}}^{3}+{{x}_{1}}^{2}{{x}_{2}}^{2}=17$.
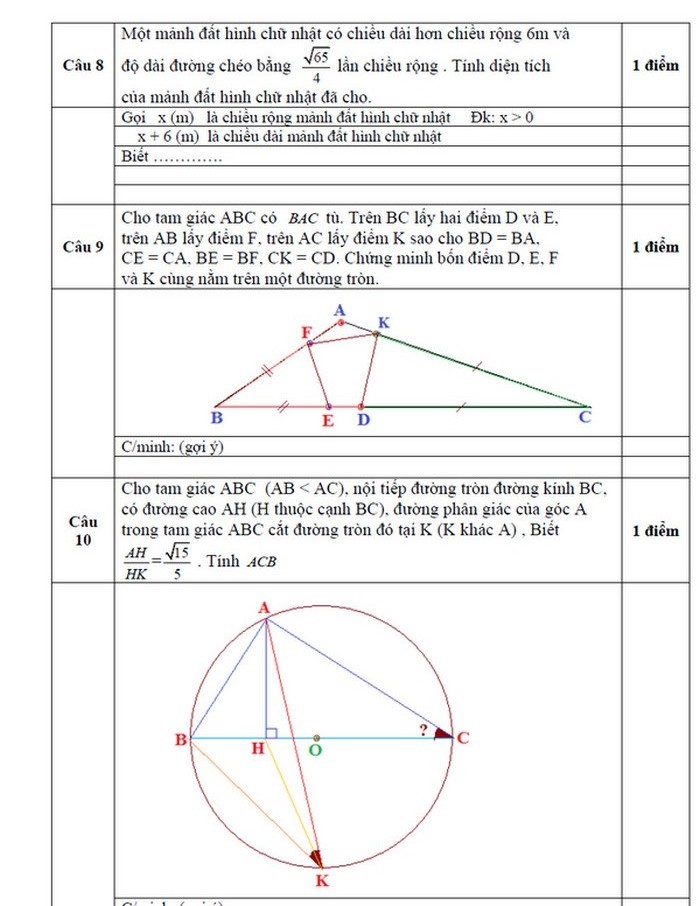
Câu 8: (1,0 điểm) Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 6m và độ dài đường chéo bằng $ \frac{\sqrt{65}}{4}$ lần chiều rộng . Tính diện tích của mảnh đất hình chữ nhật đã cho.
Câu 9: (1,0 điểm) Cho tam giác ABC có $ \widehat{BAC}$ tù. Trên BC lấy hai điểm D và E, trên AB lấy điểm F, trên AC lấy điểm K sao cho BD = BA, CE = CA, BE = BF, CK = CD. Chứng minh bốn điểm D, E, F và K cùng nằm trên một đường tròn.
Câu 10: (1,0 điểm) Cho tam giác ABC (AB < AC), nội tiếp đường tròn đường kính BC, có đường cao AH (H thuộc cạnh BC), đường phân giác của góc A trong tam giác ABC cắt đường tròn đó tại K (K khác A) , Biết $ \frac{AH}{HK}=\frac{\sqrt{15}}{5}$ . Tính $ \widehat{ACB}$.
ĐÁP ÁN ĐỀ THI TOÁN VÀO LỚP 10 TỈNH TÂY NINH 2017-2018
