Đề kiểm tra 45 phút Hình học 9 tiết 19 THCS Tân Định 2013-2014

Đề kiểm tra 1 tiết môn Hình học 9 tiết 19 trường THCS Tân Định năm học 2013-2014. Thời gian làm bài 45 phút.

A. TRẮC NGHIỆM (1 điểm)

Hướng dẫn: Nếu chọn câu 1 đáp án A đúng thì ghi vào giấy kiểm tra là: Câu 1: A

Câu 1: Tỉ số lượng giác của: $\sin {25}^0,\sin {79}^0,\sin {55}^0,cos{71}^0,cos{36}^0$ theo thứ tự từ lớn đến nhỏ là:

A. $\sin {25}^0,\cos {36}^0,\sin {55}^0,\cos {71}^0,\sin {79}^0$

B. $\sin {79}^0,\sin {55}^0,\cos {36}^0,\sin {25}^0,\cos {71}^0$

C. $\cos {71}^0,\sin {25}^0,\cos {36}^0,\sin {55}^0,sin{79}^0$

D. $\cos {71}^0,\sin {25}^0,\cos {36}^0,\sin {55}^0,\sin {79}^0$

Câu 2: Cho $0^0<\alpha <{90}^0$. Trong các đẳng thức sau, đẳng thức nào sai?

A. ${\sin }^2\alpha +{\cos }^2\alpha =1$

B. $\tan \alpha =\cot \left({90}^0-\alpha \right)$

C. $\cot \alpha =\sin \left(90-\alpha \right)$

D. $\tan \alpha .\cot \alpha =1$

Câu 3:

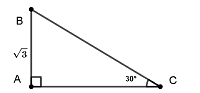
Cho tam giác ABC vuông tại A. Số đo góc C bằng ${30}^0$. Độ dài cạnh AB là $\sqrt{3}$. Độ dài BC bằng:

A. $30\sqrt{3}$

B. $3\sqrt{2}$

C. $2\sqrt{2}$

D. $2\sqrt{3}$

Câu 4:

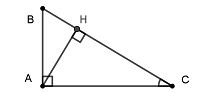
Trong hình bên, cosB = …..

A. $\frac{AH}{AB}$

B. $\sin \widehat{HAC}$

C. $\frac{AH}{AC}$

D. $\frac{AC}{BC}$

B. TỰ LUẬN

Câu 1: (2 điểm) Không dùng máy tính bỏ tủi

a) So sánh $\sin {45}^0$ và $\cos {60}^0$

b) Tính giá trị của biểu thức:

$A={\sin }^2{32}^0+{\sin }^2{58}^0+2\cot {20}^0.\cot {70}^0$

Quy ước làm tròn trong các Câu 2, Câu 3, Câu 4

+) Số đo góc làm tròn đến độ

+) Số đo độ dài làm tròn đến chữ số thập phân thứ 2

Câu 2: (2 điểm) Giải $\mathrm{\Delta }ABC$ vuông tại A, biết BC = 8 cm và $\hat{C}={35}^0$

Câu 3: (1,5 điểm) Cho tam giác ABC vuông tại A. Biết $\sin B=\frac{1}{2}$. Tính $\cos B,\tan B,\cot C$

Câu 4: (3 điểm) Cho tam giác ABC vuông tại A, AH là đường cao ứng với cạnh huyền của tam giác.

a) Cho AC = 3cm, BC = 5cm. Tính độ dài các đoạn thẳng AB, AH, BH, CH.

b) Đường thẳng qua C và song song với AB cắt AH tại D. Chứng minh ${\displaystyle AH.AD+BH.BC=B{C}^2}$

Câu 5: (0,5 điểm) Cho hình chữ nhật ABCD co AB = 2AD, một đường thẳng đi qua A cắt cạnh BC tại M, cắt đường thẳng CD tại N. Chứng minh $\frac{4}{A{B}^2}=\frac{4}{A{M}^2}+\frac{1}{A{N}^2}$