- Phương pháp chứng minh hai đường thẳng song song
- 8 cách chứng minh 2 đường thẳng song song
- 10 cách chứng minh hai đường thẳng vuông góc
- 10 cách chứng minh 3 điểm thẳng hàng
- 13 cách chứng minh hai góc bằng nhau
- 8 cách chứng minh tia Oz là tia phân giác của góc xÔy
- 7 cách chứng minh M là trung điểm của đoạn thẳng AB
- Phương pháp chứng minh các tam giác đặc biệt
- Cách xác định tâm đường tròn nội tiếp, ngoại tiếp tam giác
- Phương pháp chứng minh các tứ giác đặc biệt
- 6 cách chứng minh tứ giác nội tiếp đường tròn
- Phương pháp chứng minh đường trung trực của đoạn thẳng
- 2 cách chứng minh đường thẳng là tiếp tuyến của đường tròn
- 4 cách chứng minh hai cung tròn bằng nhau
- 15 cách chứng minh hai đoạn thẳng bằng nhau
- 7 cách chứng minh một đoạn thẳng bằng 1/2 đoạn thẳng khác
- 4 cách chứng minh một góc bằng nửa góc khác
- 5 cách chứng minh 3 đường thẳng đồng quy
- Cách chứng minh hai tam giác đồng dạng và ứng dụng
- Ví dụ cách chứng minh hai tam giác bằng nhau
- Cách chứng minh một điểm là trọng tâm, trực tâm của tam giác
- Chứng minh một điểm là tâm đường tròn ngoại tiếp, nội tiếp, bàng tiếp tam giác
- Chứng minh các quan hệ không bằng nhau (cạnh – góc – cung)
Toán cấp 2 hướng dẫn các em phương pháp, cách xác định tâm đường tròn nội tiếp và đường tròn ngoại tiếp tam giác qua các khái niệm.
Để không bị nhầm lẫn và hiểu rõ hơn về đường tròn nội tiếp, ngoại tiếp tam giác thì các em cần tìm hiểu qua các khái niệm.
1. Khái niệm đường tròn nội tiếp, ngoại tiếp tam giác
– Khi 3 cạnh của tam giác là tiếp tuyến của đường tròn và đường tròn nằm trong tam giác thì ta gọi đường tròn đó là đường tròn nội tiếp tam giác.
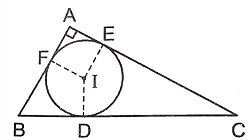
Đường tròn tâm I nội tiếp tam giác ABC
– Đường tròn ngoại tiếp tam giác là đường tròn đi qua cả 3 đỉnh của tam giác. Có thể nói cách khác là tam giác nội tiếp đường tròn.
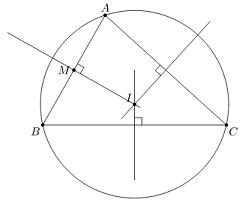
Đường tròn tâm I ngoại tiếp tam giác ABC
2. Cách xác định tâm đường tròn nội tiếp, ngoại tiếp tam giác
Để xác định được tâm của đường tròn nội tiếp và tâm đường tròn ngoại tiếp tam giác các em cần ghi nhớ lý thuyết:
– Tâm đường tròn nội tiếp của tam giác là giao điểm ba đường PHÂN GIÁC TRONG của tam giác (có thể là 2 đường phân giác)
– Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường TRUNG TRỰC của ba cạnh tam giác (có thể là giao điểm hai đường trung trực)