Các dạng toán về lũy thừa với số mũ tự nhiên. Nhân hai lũy thừa cùng cơ số –
Toán lớp 6
A. TÓM TẮT LÍ THUYẾT.
1. Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a :
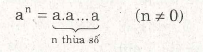
a : Cơ số ; n : số mũ
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
Quy ước : a1 = a.
2. Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ :
am.an =am+n .
B. CÁC DẠNG TOÁN.
Dạng 1. VIẾT GỌN MỘT TÍCH BẰNG CÁCH DÙNG LŨY THỪA
Phương pháp giải
Áp dụng công thức:
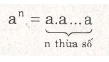
Ví dụ 1. (Bài 56 trang 27 SGK)
Viết gọn các tích sau bằng cách dùng lũy thừa :
a) 5.5.5 5.5.5 ; b) 6.6.6.3.2 ;
c) 2 2.2.3.3 ; d) 100.10.10.10.
Giải
a) 5.5.5.5.5.5 = 56
b) 6.6.3.2 = 6.6.6.6 = 64 ;
c) 2.2.3.3 = 23.32 ;
d) 100.10.10.10 = 10.10.10.10.10 = 105 .
Ví dụ 2. (Bài 57 trang 28 SGK)
Tính giá trị các lũy thừa sau :
a) 23, 24,25,26,27,28,29,210 ;
b) 32, 33,34,35 ;
c) 42,43,44;
d) 52,53,54;
e) 62, 63,64.
Giải
a) 23 = 2.2.2 = 8 ; 24 = 23.2 = 8.2 = 16.
Làm tương tự như trên ta được :
25 = 32 , 26 = 64 , 27 = 128 , 28 = 256, 29 = 512 , 210 = 1024.
b) 32 = 9, 33 = 27 , 34 = 81, 35 = 243 .
c) 42 = 16, 43 = 64, 44 = 256 .
d) 52 = 25, 53 = 125, 54 = 625.
e) 62 = 36, 63 = 216, 64 = 1296.
Ví dụ 3. (Bài 58a và 59a trang 28 SGK)
58a) Lập bảng bình phương của các số tự nhiên từ 0 đến 20.
59a) Lập bảng lập phương của các số tự nhiên từ 0 đến 10.
Giải
58a) Lập bảng bình phương của các số tự nhiên từ 0 đến 20.
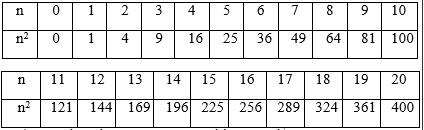
59a) Lập bảng lập phương của các số tự nhiên từ 0 đến 10.

Ví dụ 4. Nhà văn Anh sếch-xpia (1564-1616) đã viết a2 cuốn sách, trong đó a là số tự
nhiên lớn nhất có hai chữ số.
Tính số sách sếch-xpia đã viết.
Giải
Số tự nhiên lớn nhất có hai chữ số là 99 nên a = 99. Do đó a2 = 992 = 9801.
Số sách sếch-xpia đã viết là 9801 cuốn.
Ví dụ 5. (Bài 62a trang 28 SGK)
Tính 102 ; 103 ; 104 ; 105 ; 106.
Đáp số
102 = 100 ; 103 = 1000 ; 104 = 10000 ; 105 = 100000 ; 106 = 1000 000.
Ví dụ 6. (Bài 65 trang 29 SGK)
Bằng cách tính, em hãy cho biết số nào lớn hơn trong hai số sau ?
a) 23 và 32 ; b) 24 và 42 ;
c)25 và 52; d) 210 và 100.
Giải
a) 23 = 8, 32 = 9 . Vì 8 < 9 nên 23 < 32 .
b) 24 =16 , 42=16 nên 24 = 42.
c) 25 = 32 , 52 = 25 nên 25 > 52.
d) 210 = 1024 nên 210 >100.
Ví dụ 7. (Bài 66 trang 29 SGK)
Đố : Ta biết 112 =121 ; 1112 =12321. Hãy dự đoán : 1111a bằng bao nhiêu ? Kiểm tra lại dự
đoán đó.
Đáp số
11112 = 1234321.
Dạng 2. VIẾT MỘT SỐ DƯỚI DẠNG MỘT LŨY THỪA VỚI SỐ MŨ LỚN HƠN 1
Ví dụ 8. (Bài 58 b; 59b trang 28 SGK)
58b) Viết mỗi số sau thành bình phương của một số tự nhiên : 64 ; 169 ; 196.
59b) Viết mỗi số sau thành lập phương của một số tự nhiên : 27 ; 125 ; 216.
Giải
58b) 64 = 8.8 = 82; 169 = 13.13 = 132 ; 196 = 14.14 = 142.
59b) 27 = 3.3,3 = 33 ; 125 = 5.5.5 = 53 ; 216 = 6.6.6 = 63.
Ví dụ 9. (Bài 61 trang 28 SGK)
Trong các số sau, số nào là lũy thừa của một số tự nhiên với số mũ lớn hơn 1 (chú ý rằng
có những số có nhiều cách viết dưới dạng lũy thừa) : 8, 16, 20, 27, 60, 64, 81, 90, 100.
Đáp số
8 = 23; 16 = 42 = 24 ;
27 = 33 ; 64 = 82 – 26 = 43;
81 = 92 = 34; 100 = 102.
Ví dụ 10. (Bài 62b trang 28 SGK)
Viết mỗi số sau dưới dạng lũy thừa của 10 : 1000 ; 1 000 000;
![]()
Đáp số
1000 = 103;
1 000 000 = 106;
1 tỉ = 109;
![]()
Dạng 3. NHÂN HAI LŨY THỪA CÙNG CƠ SỐ
Phương pháp giải
Áp dụng công thức : am.an = am+n (a,m,n ∈ N).
Ví dụ 11. (Bài 60 trang 28 SGK)
Viết kết quả phép tính sau dưới dạng một lũy thừa :
a) 33.34 ; b) 52.57; c) 75.7.
Giải
a) 33.34 = 33+4 = 37 ;
b) 52.57 = 52+7 = 59 ;
c) 75.7 = 75+1 – 76
Ví dụ 12. (Bài 63 trang 28 SGK)
Điền dấu “ x ” vào ô thích hợp :

Giải

Ví dụ 13. (Bài 64 trang 29 SGK)
Viết kết quả phép tính dưới dạng một lũy thừa :
a) 23.22.24;
b) 102.103.105 ;
c) x . x5 ;
d) a3.a2.a5 ;
Giải
a) 23.22.24 = 23+2+4 = 29 ;
b) 102.103.105 = 102+3+5 = 1010;
c) x = x5 = x1+5 – x6;
d) a3.a2.a5 = a3+2+5 = 210 ;
>> Phần tiếp theo: