Các dạng toán về phép trừ và phép chia – Toán lớp 6
A. TÓM TẮT LÍ THUYẾT.
1. Phép trừ hai số tự nhiên :
Cho hai số tự nhiên a và b. Nếu có số tự nhiên x sao cho b x = a
thì ta có phép trừ a – b – x.
Điều kiện để thực hiện được phép trừ là số bị trừ lớn hơn hoặc bằng số trừ.
2. Phép chia hết và phép chia có dư:
Cho hai số tự nhiên a và b trong đó b ≠ 0. Ta luôn tìm được các số tự nhiên duy nhất q và r
sao cho :
a = b . q r (0 ≤ r ≤ b)
(số bị chia) = (số chia). (thương) (số dư)
Số chia bao giờ cũng khác 0. số dư bao giờ cũng nhỏ hơn số chia. Nếu r = 0 thì ta có a =
b.q và được phép chia hết.
Như vậy, điều kiện để a chia hết cho b ( a,b ∈ N, b ≠ 0 ) là có số tự nhiên q sao cho a = b.q.
Nếu r ≠ 0 thì ta được phép chia có dư.
B. CÁC DẠNG TOÁN.
Dạng 1. THỰC HÀNH PHÉP TRỪ VÀ PHÉP CHIA
Phương pháp giải
– Có thể trừ theo “hàng ngang” hoặc viết số trừ dưới số bị trừ sao cho các chữ số cùng hàng
thì thẳng cột với nhau rồi trừ từ phải sang trái.
– Đặt phép chia và thử lại kết quả bằng phép nhân.
– Sử dụng máy tính bỏ túi (đổi với những bài được phép dùng).
Ví dụ 1. (Bài 41 trang 22 SGK)
Hà Nội, Huế, Nha Trang, Thành phố Hồ Chí Minh nằm trên quốc lộ 1 theo thứ tự như
trên. Cho biết các quãng đường trên quốc lộ ấy :
Hà Nội – Huế : 658 km ;
Hà Nội – Nha Trang : 1278 km ;
Hà Nội – Thành pho Hồ Chí Minh : 1710 km ;
Tính các quãng đuờng : Huế – Nha Trang, Nha Trang – Thành phô” Hồ Chí Minh.
Giải
Quãng đường Huế – Nha Trang :
1278 – 658 = 620 (km).
Quãng đường Nha Trang – Thành phố Hồ Chí Minh :
1710 – 1278 = 432 (km).
Ví dụ 2. (Bài 42 trang 23 SGK)
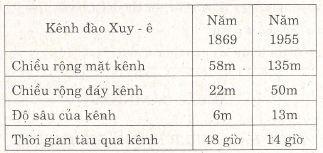
Các số liệu về kênh đào Xuy-ê (Ai Cập) nối Địa Trung Hải và Hồng Hải được cho trong
bảng 1 và bảng 2.
Bảng 1 :
Bảng 2:
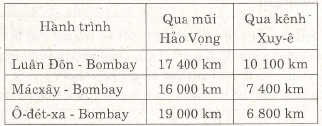
a) Trong bảng 1 các số liệu ở năm 1955 tăng thêm (hay giảm bớt) bao nhiêu so với năm 1869
(năm khánh thành kênh đào)?
b) Nhờ đi qua kênh đào Xuy-ê, mỗi hành trình trong bảng 2 giảm bớt được bao nhiêu kilômét ?
Giải
a) Chiều rộng mặt kênh tăng : 135 – 58 = 77 (m)
Chiều rộng đáy kênh tăng : 50 – 22 = 28 (m)
Độ sâu của kênh tăng : 13 – 6 = 7 (m)
Thời gian tầu qua kênh giảm : 48 – 14 = 34 (giơ).
b) Hành trình Luân Đôn – Bombay giảm :
17400 – 10100 = 7300 (km)
Hành trình Macxây – Bombay giảm :
16000 – 7400 = 8600 (km).
Hành trình ô-đét-xa – Bombay giảm :
19000-6800 = 12200 (km).
Ví dụ 3. (Bài 43 trang 23 SGK)
Tính khối lượng quả bí ở hình 18 khi cân thăng bằng .
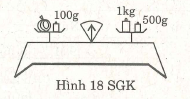
Giải
Gọi khối lượng quả bí là x (g) (x > 0), ta có :
x 100 = 1000 500
x = 1000 500 – 100
x = 1400.
Vậy khôi lượng quả bí là 1400g.
Ví dụ 4. (Bài 51 trang 25 SGK)
Đố : Điền số thích hợp vào ô vuông sao cho tổng các số ở mỗi hàng, ở mỗi cột, ở mỗi đường
chéo đều bằng nhau.
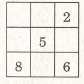
Giải
Gọi các số phải tìm ở các ô trống là x, y, z, t, u (xem hình vẽ).
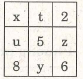
Tổng các số ở mỗi hàng, ở mỗi cột, ở mỗi đường chéo bằng : 8 5 2 = 15
Do đó, ta có :
y = 15 – 8 – 6 = 1 ;
z = 15 – 6 – 2 = 7 ;
t = 15 – 5 -1 = 9 ;
u= 15 – 5 – 7 = 3;
x = 15 – 9 – 2 = 4.
Vậy ta được bảng dưới .

Ví dụ 5. (Bài 50 trang 24 SGK)
Dùng máy tính bỏ túi để tính :
425 – 257 ; 91 – 56 ; 82 – 56 ; 73 – 56 ; 652 – 46 – 46 – 46.
Giải
Đáp số : 168; 35; 26; 17; 514.
Chú ý: Máy tính SHARP TK – 340 và một số máy tính bỏ túi thông thường khác cho ta cách
trừ đi một số nhiều lần :
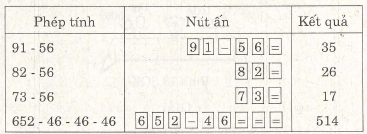
Ví dụ 6. (Bài 55 trang 25 SGK)
Dùng máy tính bỏ túi :
– Tính vận tốc của một ô tô biết rằng trong 6 giờ ô tô đi được 288km.
– Tính chiều dài miếng đất hình chữ nhật có diện tích 1530m2 , chiềụ rộng 34m.
Giải
Đáp số: 48km/h ; 45m.
Dạng 2. ÁP DỤNG TÍNH CHẤT CÁC PHÉP TÍNH ĐỂ TÍNH NHANH
Phương pháp giải
Áp dụng một số tính chất sau đây :
– Tổng của hai số không đổi nếu ta thêm vào ở số hạng này và bớt đi ở số hạng kia cùng
một số đơn vị.
Ví dụ : 99 48 = (99 1) (48 – 1) = 100 47 = 147.
– Hiệu của hai số không đổi nếu ta thêm vào một số bị trừ và số trừ cùng một số đơn vị.
Ví dụ : 316 – 97 = (316 3) – (97 3) = 319 – 100 = 219.
– Tích của hai số không đổi nếu ta nhân thừa số này và chia thừa số kia cho cùng một số.
Ví dụ : 25 . 12 = (25 . 4).(12 : 4) = 100.3 = 300
– Thương của hai số không đổi nếu ta nhân cả số bị chia và số chia vói cùng một sô.
Ví dụ : 1200 : 50 = (1200.2) : (50.2) = 2400 : 100 = 24.
– Chia một tổng cho một số (a b) : c = a : c b : c ( truờng hợp chia hết).
Ví dụ : 276 : 23 = (230 46) : 23 = 230 : 23 46 : 23 = 10 2 = 12.
Ví dụ 7. (Bài 48 trang 24 SGK)
Tính nhẩm : 35 98 ; 46 29.
Giải
35 98 = (35 – 2) (98 2) = 33 100 = 133.
46 29 = (46 – 1) (29 1) = 45 30 = 75.
Ví dụ 8. (Bài 49 trang 24 SGK)
Tính nhẩm : 321 – 96 ; 1354 – 997.
Giải
321 – 96 = (321 4) – (96 4) = 325 – 100 = 225.
1354 – 997 = (1354 3) – (997 3) = 1357 – 1000 = 357.
Ví dụ 9. (Bài 52 trang 25 SGK)
Tính nhẩm :
a) 50 ; 16.25 ;
b) 2100 : 50 ; 1400 : 25 ;
c) 132 : 12 ; 96 : 8.
Giải
a) 50 = (14 : 2). (50.2) = 7.100 = 700.
16.25 = (16 : 4). (25.4) = 4.100 = 400.
b) 2100 : 50 = (2100.2) : (50.2) = 4200 : 100 = 42.
1400 : 25 = (1400.4) : (25.4) = 5600 : 100 = 56.
c) 132 :12 = (120 12) : 12 = 120 :12 12 :12 = 10 1 = 11.
96 : 8 = (80 16) : 8 = 80 : 8 16 : 8 = 10 2 = 12.
Dạng 3. TÌM SỐ CHƯA BIẾT TRONG MỘT ĐẲNG THỨC
Phương pháp giải
– Muốn tìm một số hạng trong phép cộng hai số’, ta lấy tổng trừ số hạng kia ;
– Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ ;
– Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu ;
– Muốn tìm số bị chia, ta lấy thương nhân với số chia ;
– Muốn tìm số chia, ta lấy số bị chia chia cho thương.
Ví dụ 10. (Bài 44 trang 24 SGK)
Tìm x, biết :
a) x : 13 = 41 ; b) 1428 : x = 14 ; c) 4x : 17 = 0 ;
c) 7x – 8 = 713 ; e) 8 (x – 3) = 0 ; g) 0 : x = 0.
Giải
a) x = 41.13 = 533 ;
b) x = 1428 : 14 = 102;
c) 4x = 0.17 => 4x = 0 => x = 0 ;
d)7x – 8 = 713 ;
7x = 713 8
x = 721 : 7
x = 103.
e) 8( x – 3 ) = 0
x – 3 = 0
x = 3.
g) 0 : x = 0 => x là số bất kì khác 0.
Ví dụ 11. (Bài 47 trang 24 SGK)
Tìm số tự nhiên x biết :
a) (x – 35) – 120 = 0 ;
b) 124 (118 – x) = 217 ;
c) 156 – (x 61) = 82.
Giải
a) (x – 35) – 120 = 0
x – 35 = 120
x = 120 35
x = 155.
b) 124 (118 – x) = 217
118 – x =217 – 124
118 – x =93
x = 118 – 93
x = 25.
c) 156 – (x 61) = 82
x 61 = 156 – 82
x 61 = 74
x= 74-61
x = 13.
Dạng 4. BÀI TẬP VỀ PHÉP CHIA CÓ DƯ
Phương pháp giải
Sử dụng định nghĩa của phép chia có dư và công thức :
a = b.q r (0 < r < b)
Từ công thức trên suy ra : b = (a – r): q ; q = (a – r): b ; r = a – b.q.
Ví dụ 12. (Bài 45 trang 24 SGK)
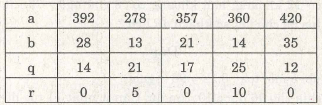
Điền vào ô trống sao cho a = b.q r với 0 < r < b :
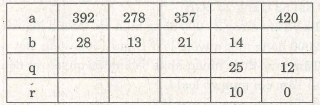
Ở cột số thứ nhất, ta có : 392 : 28 = 14 nên q = 14 , r = 0.
Ở cột số thứ hai, ta có : 278 : 13 = 21 (dư 5) nên q = 21, r = 5.
Ở cột số thứ ba, ta có : 357 : 21 = 17 nên q = 17, r = 0
Ở cột số thứ tư, ta có : a = 14.25 10 = 360.
Ở cột số thứ năm, ta có : b = (a – r): q = (420 – 0): 12 = 35.
Vậy ta có bảng đầy đủ sau :
Ví dụ 13. (Bài 46 trang 24 SGK)
a) Trong phép chia cho 2, số dư có thể bằng 0 hoặc 1. Trong mỗi phép chia cho 3, cho 4, cho
5, số dư có thể bằng bao nhiêu ?
b) Dạng tổng quát của số chia hết cho 2 là 2k, dạng tổng quát của số chia cho 2 dư 1 là 2k 1
với k ∈ N . Hãy viết dạng tổng quát của số chia hết cho 3, số chia cho 3 dư 1, sô” chia cho 3
dư 2.
Giải
a) Trong phép chia cho 3, số dư có thể bằng 0, 1, 2.
Trong phép chia cho 4, số dư có thể bằng 0, 1, 2, 3.
Trong phép chia cho 5, số dư có thể bằng 0, 1, 2, 3, 4.
c) Dạng tổng quát của số chia hết cho 3 là 3k ; dạng tổng quát của số chia cho 3 dư 1 là 3k
1 ; dạng tổng quát của số chia cho 3 dư 2 là 3k 2 (k ∈ N).
Ví dụ 14. (Bài 53 trang 25 SGK)
Bạn Tâm dùng 21 000 đồng mua vở. Có hai loại vở : loại I giá 2000 đồng một quyển, loại II
giá 1500 đồng một quyển. Bạn Tâm mua được nhiều nhất bao nhiêu quyển vở nếu :
a) Tâm chỉ mua vở loại I ?
b) Tâm chỉ mua vở loại II ?
Đáp án:
a) 21 000 chia cho 2000 được 10, còn dư . Tâm mua được nhiều nhất 10 quyển vở loại I.
b) 14 quyển vở loại II.
Ví dụ 15. (Bài 54 trang 25 SGK)
Một tàu hỏa cần chở 1000 khách du lịch. Biết rằng mỗi toa có 12 khoang, mỗi khoang có 8
chỗ ngồi, cần ít nhất mấy toa để chở hết số khách du lịch ?
Đáp án:
Số người ở mỗi toa : 8.12 = 96 (người).
1000 chia cho 96 được 10, còn dư. cần ít nhất 11 toa để chở hết số khách.
Dạng 5. TÌM NHỮNG CHỮ SỐ CHƯA BIẾT TRONG PHÉP TRỪ VÀ PHÉP CHIA
Phương pháp giải
– Đối với phép trừ, tính lần lượt theo cột từ phải sang trái, chú ý những trường hợp có “nhớ”.
– Đối với phép chia, đặt tính và lần lượt thực hiện phép chia.
Ví dụ 16. Thay dấu * bằng những chữ số thích hợp :
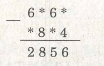
Giải
Ở cột hàng đơn vị có * – 4 ta được chữ số 6 thì * chỉ có thể là 0 (vì 10 – 4 = 6) và có “nhớ” 1 sang cột hàng chục ;
Ở cột hàng chục có 6 – (* 1 “nhớ”) được chữ số 5 thì * chỉ có thể là 0 ;
Ở cột hàng trăm có * – 8 được chữ số 8 thì * chỉ có thể là 6 (để có 16 – 8 = 8) và có “nhớ” 1 sang cột hàng nghìn ;
Ở cột hàng nghìn có 6 – (* 1 “nhớ”) được chữ số 2 thì * chỉ có thể là 3.
Vậy ta có phép trừ :
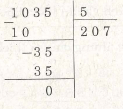
Ví dụ 17. Thay dấu * bằng những chữ sô” thích họp :
Giải
Chia 10 cho số chia * được 2 không dư, vậy * ở sô” chia là 5. Khi đó ta có :
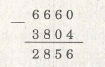
Khi hạ dấu * ở hàng chục của số bị chia xuống thì không chia được cho 5 nên chữ số hàng
chục ở thương phải bằng 0. Vậy thương bằng 207, do đó số bị chia là 207.5 = 1035. Ta có phép chia: