Các dạng toán về tính chất chia hết của một tổng – Toán lớp 6
A. TÓM TẮT LÍ THUYẾT.
Tính chất 1 : Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì
tổng chia hết cho số đó.
a chia hết cho m,b chia hết cho m,c chia hết cho m
=> (a b c) chia hết cho m
Chú ý: Tính chất 1 cũng đúng đối với một hiệu (a ≥ b):
a chia hết cho m, b chia hết cho m=>(a-b) chia hết cho m.
Tính chất 2 : Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số
hạng khác đều chia kết cho số đó thì tổng không chia hết cho số đó :
a không chia hết cho m , b không chia hết cho m , c không chia hết cho m
=> (a b c) không chia hết cho m
Chú ý :Tính chất 2 cũng đúng đối với một hiệu ( a > b ) :
a không chia hết cho m và b chia hết cho m => (a – b) không chia hết cho m .
a không chia hết cho m va b không chia hết cho m=>(a-b) không chia hết cho m.
B. CÁC DẠNG TOÁN.
Dạng 1. XÉT TÍNH CHIA HẾT CỦA MỘT TỔNG HOẶC MỘT HIỆU
Áp dụng tính chất 1 và tính chất 2 về sự chia hết của một tổng, một hiệu.
Ví dụ 1. (Bài 83 trang 35 SGK)
Áp dụng tính chất chia hết, xét xem mỗi tổng sau có chia hết cho 8 không ?
a) 48 56 ; b) 80 17.
Giải
a) 48 : 8 , 56 : 8 => (48 +56) chia hết cho 8 (Tính chất 1)
b) 80 : 8 ,17 / 8 => (80 +17) không chia hết cho 8 (Tính chất 2).
Ví dụ 2. (Bài 84 trang 35 SGK)
Áp dụng tính chất chia hết, xét xem hiệu nào chia hết cho 6 ?
a) 54 – 36 ; b) 60 – 14.
Trả lời
(54 – 36) chia hết cho 6.
Ví dụ 3. (Bài 85 trang 36 SGK)
Áp dụng tính chất chia hết, xét xem tổng nào chia hết cho 7 ?
a) 35 +49 +210 ; b) 42 +50 +140 ; c) 560 +18 +3.
Trả lời
(35 +49 +210) : 7 ; (560 +18 +3) ; 7 .
Ví dụ 4. (Bài 86 trang 36 SGK)
Điền dấu “x ” vào ô thích hợp trong các câu sau và giải thích điều đó :

Giải
a) 4134.4 chia hết cho 4 , 16 chia hết cho 4 => (134.4 +16) chia hết cho 4;
b) 21.8 chia hết cho 8 , 17 không chia hết cho 8 => (21.8 +17) không chia hết cho 8 ;
c) 3.100 chia hết cho 6, 34 không chia hết cho 6 =>(3.100 +34) không chia hết cho 6
Do đó, ta điền dấu “x ” như sau :

Ví dụ 5. (Bài 88 trang 36 SGK)
Khi chia số tự nhiên a cho 12, ta được số dư là 8. Hỏi số a có chia hết cho 4 không ? Có chia
hết cho 6 không ?
Hướng dẫn : Viết a = 12 .q +8 (q ∈ N) rồi áp dụng tính chất chia hết của tổng.
Trả lời
a chia hết cho 4, không chia hết cho 6.
Ví dụ 6. (Bài 89 trang 36 SGK)
Điền dấu “x ” vào ô thích hợp trong các câu sau ;
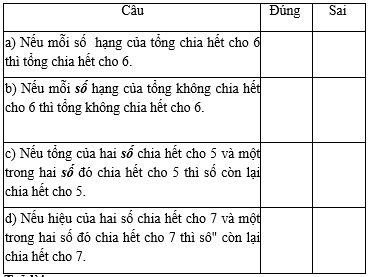
Trả lời
a) Đúng ; b) Sai ; c) Đúng ; d) Đúng.
Ví dụ 7. (Bài 90 trang 36 SGK)
Gạch dưới số mà em chọn :
Nếu a chia hết cho 3 và b chia hết cho 3 thì tổng a b chia hết cho 6 ; 9 ; 3.
Nếu a chia hết cho 2 và b chia hết cho 4 thì tổng a b chia hết cho 4 ; 2 ; 6.
Nếu a chia hết cho 6 và b chia hết cho 9 thì tổng a b chia hết cho 6 ; 3 ; 9.
Trả lời
Tổng chia hết cho 3. (gạch dưới số 3).
Tổng chia hết cho 2. (gạch dưới số 2).
Tổng chia hết cho 3. (gạch dưới sô 3).
Dạng 2. TÌM ĐIỀU KIỆN CỦA MỘT SỐ HẠNG ĐỂ TỔNG HOẶC HIỆU CHIA
HẾT CHO MỘT SỐ NÀO ĐÓ.
Phương pháp giải
Áp dụng tính chất 1 và tính chất 2 để tìm điều kiện của số hạng chưa biết.
Ví dụ 8. (Bài 87 trang 36 SGK)
Cho tổng A = 12 14 16 X với x ∈ N. Tìm x để :
a) A chia hết cho 2 ;
b) A không chia hết cho 2.
Giải
Ta có nhận xét :
12 chia hết cho 2 ,
14 chia hết cho 2 ,
16 chia hết cho 2. Do đó :
Nếu x là số chẵn thì theo tính chất 1, A chia hết cho 2 ;
Nếu x là số lẻ thì theo tính chất 2, A không chia hết cho 2.
Dạng 3. XÉT TÍNH CHIA HẾT CỦA MỘT TÍCH
Phương pháp giải
Áp dụng tính chất : Nếu trong một tích các số tự nhiên có một thừa số chia hết cho một
số nào đó thì tích cũng chia hết cho số đó.
Ví dụ 9. Số 15 = 3.5 chia hết cho 3 và cho 5.
Các tích 4.15, 7.45, 11.750 có chia hết cho 3 không ? Cho 5 không ?
Giải
Ta có thể viết : 7.45 = 7.3.15 ; 11.750 = 11.10.5.15 .
4.15 , 7.45 , 11. 750 là các tích gồm nhiều thừa số, tích nào cũng có ít nhất một thừa số là
15, 15 chia hết cho 3 và cho 5 nên các tích trên đều chia hết cho 3 và cho 5.