Ôn tập: Diện tích các hình trong không gian

Đây là bài thứ 23 of 23 trong series Ôn tập Hình học 9

Để có thể tính được diện tích các hình trong không gian: Hình trụ, hình nón, hình nón cụt và hình cầu thì các em cần phải nắm được các công thức.

Các công thức tính diện tích cần ghi nhớ là:

1. Công thức tính diện tích hình trụ

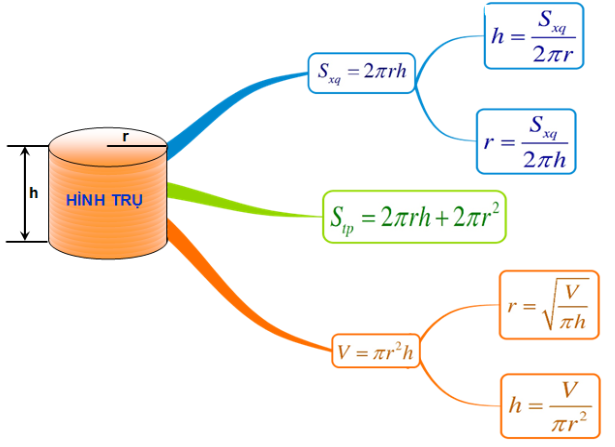
2. Công thức tính diện tích hình nón, nón cụt

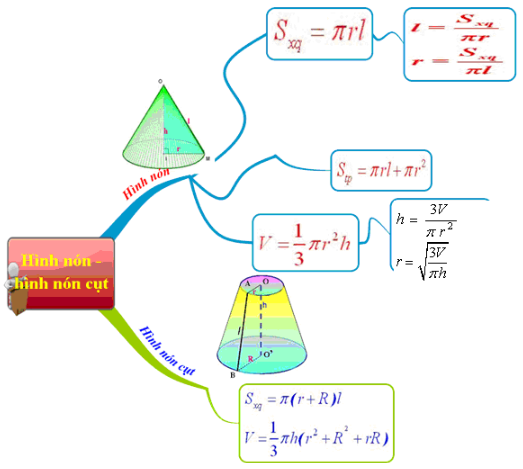
3. Công thức tính diện tích hình cầu

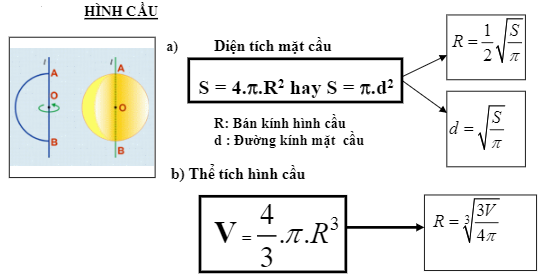
Ví dụ minh họa:

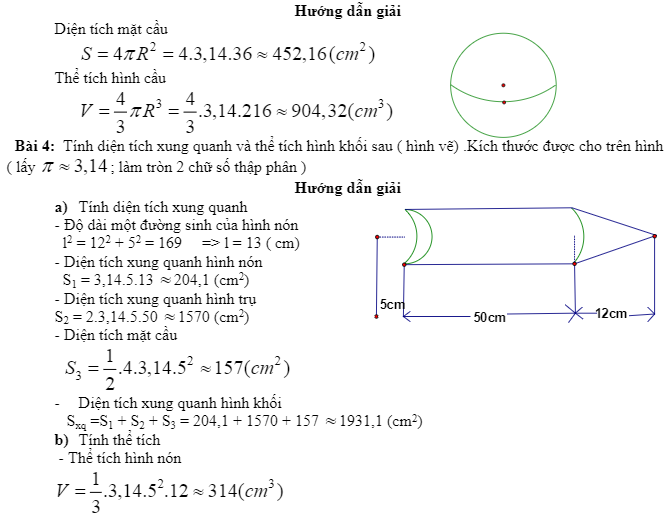
Bài tập tự giải tính diện tích các hình trong không gian:

Bài 1:

Cho hình hộp chữ nhật ABCDA’B’C’D’. Biết AB = 4 cm; AC = 5 cm và A’C = 13 cm. Tính thể tích và diện tích xung quanh của hình hộp chữ nhật đó.

Bài 2:

Cho hình lập phương ABCDA’B’C’D’ có diện tích mặt chéo ACC’A’ bằng $ \displaystyle 25\sqrt{2}$ cm². Tính thể tích và diện tích toàn phần của hình lập phương đó.

Bài 3:

Cho hình hộp chứ nhật ABCDA’B’C’D’. Biết AB = 15 cm, AC’ = 20 cm và góc A’AC’ bằng 60⁰. Tính thể tích và diện tích toàn phần của hình hộp chữ nhật đó.

Bài 4:

Cho lăng trụ đứng tam giác đều ABCA’B’C’. Tính diện tích xung quanh và thể tích của nó biết cạnh đáy dài 6 cm và góc AA’B bằng 30⁰.

Bài 5:

Cho tam giác ABC đều cạnh a. Đường thẳng d vuông góc với mặt phẳng (ABC) tại trọng tâm G của tam giác ABC. Trên đường thẳng d lấy một điểm S. Nối SA, SB, SC.

a)Chứng minh rằng SA = SB = SC.

b)Tính diện tích toàn phần và thể tích của hình chóp S.ABC, cho biết SG = 2a.

Bài 6:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là a và đường cao là $ \displaystyle \frac{a\sqrt{2}}{2}$.

a)Chứng minh các mặt bên của hình chóp là các tam giác đều.

b)Tính thể tích và diện tích xung quanh của hình chóp.

Bài 7:

Cho hình chóp tam giác đều S.ABC có cạnh đáy và cạnh bên đều bằng a.

a)Tính diện tích toán phần của hình chóp.

b)Tính thể tích của hình chóp.

Bài 8:

Cho hình chóp tứ giác đều S.ABCD có chiếu cao 15 cm và thể tích là 1280 cm³.

a)Tính độ dài cạnh đáy.

b)Tính diện tích xung quanh của hình chóp.

Bài 9:

Một hình chóp cụt diện tích đáy nhỏ là 75 cm², diện tích đáy lớn gấp 4 lần diện tích đáy nhỏ và chiều cao là 6 cm. Tính thể tích của hình chóp cụt đó.

Bài 10:

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với mặt phẳng đáy (ABCD).

a)Tính thể tích hình chóp.

b)Chứng minh rằng bốn mặt bên là những tam giác vuông.

a)Tính diện tích xung quanh của hình chóp.

Bài 11:

Một hình trụ có đường cao bằng đường kính đáy. Biết thể tích hình trụ là 128π cm³, tính diện tích xung quanh của nó.

Bài 12:

Một hình nón có bán kính đáy bằng 5 cm và diện tích xung quanh bằng 65π cm². Tính thể tích của hình nón đó.

Bài 13:

Cho hình nón cụt, bán kính đáy lớn bằng 8 cm, đường cao bằng 12 cm và đường sinh bằng 13 cm.

a) Tính bán kính đáy nhỏ.

b) Tính diện tích xung quanh và thể tích của hình nón cụt đó.

Bài 14:

Một hình cầu có diện tích bề mặt là 36π cm². Tính thể tích của hình cầu đó.

Series Navigation

<< Ôn tập: Chứng minh đường thẳng đi qua điểm cố định